電圧方程式は同期モータを記述する基本式の一つであり，モータ制御などにおいて非常に重要な役割を果たします。本記事では，非突極同期モータのインダクタンス高調波を含んだ電圧方程式のα-β座標系からd-q回転座標系への変換（Park; パーク変換）方法と，d-q回転座標系における電圧方程式の定常/非定常状態のベクトル図について解説します。
関連記事はこちら↓からどうぞ。
同期モータの電圧方程式ー②3相座標系⇒α-β座標系への変換（Clarke; クラーク変換）ー
電圧方程式は同期モータを記述する基本式の一つであり，モータ制御などにおいて非常に重要な役割を果たします。本記事では，非突極同期モータのインダクタンス高調波を含んだ電圧方程式の3相座標系からα-β座標系への変換（Clarke; クラーク変...
yuyumoyuyu.com
2020.10.18
同期モータの電圧方程式ー④d,q軸鎖交磁束を用いた導出ー
電圧方程式はモータの重要な基本式の一つです。前記事までは，d,q軸電圧方程式をd,q軸インダクタンスと界磁磁束で表現していました。必要に駆られて，d,q軸鎖交磁束を用いた電圧方程式を導出したため，備忘録的にその導出過程をまとめます。
...
yuyumoyuyu.com
2021.07.05
モータ理論式における位相角は時間？空間？
モータの理論式には様々な三角関数(sinやcos)が登場します。その位相角は時間を表現するものと空間を表現するものがあり，それらを混同して考えると理論式への理解が不十分になってしまいます。本記事では，少々ややこしい位相角に焦点を当てて解...
yuyumoyuyu.com
2020.10.04
d-q回転座標系のお話－②座標変換行列－
同期モータでは、平衡3相交流によって生じる回転磁界やロータ（回転子）と同期しながら回転するd-q回転座標系を考えます。本記事では、この3相座標系からd-q回転座標系への変換行列について説明します。
大きい画面で表示したい方はこちらからご覧...
yuyumoyuyu.com
2020.07.12
大きい画面で表示したい方はこちらからご覧ください。
スライドの目次
- 本記事を読む前に
- 同期モータの電圧方程式
- α-β座標系の電圧方程式
- α-β座標系⇒d-q回転座標系への変換
- 誘導起電力の第1項目の計算
- 誘導起電力の第2項目の計算
- 誘導起電力の第1,2項のまとめ
- 界磁磁束の計算
- d-q回転座標系における電圧方程式
- d-q回転座標系の電圧方程式の解釈
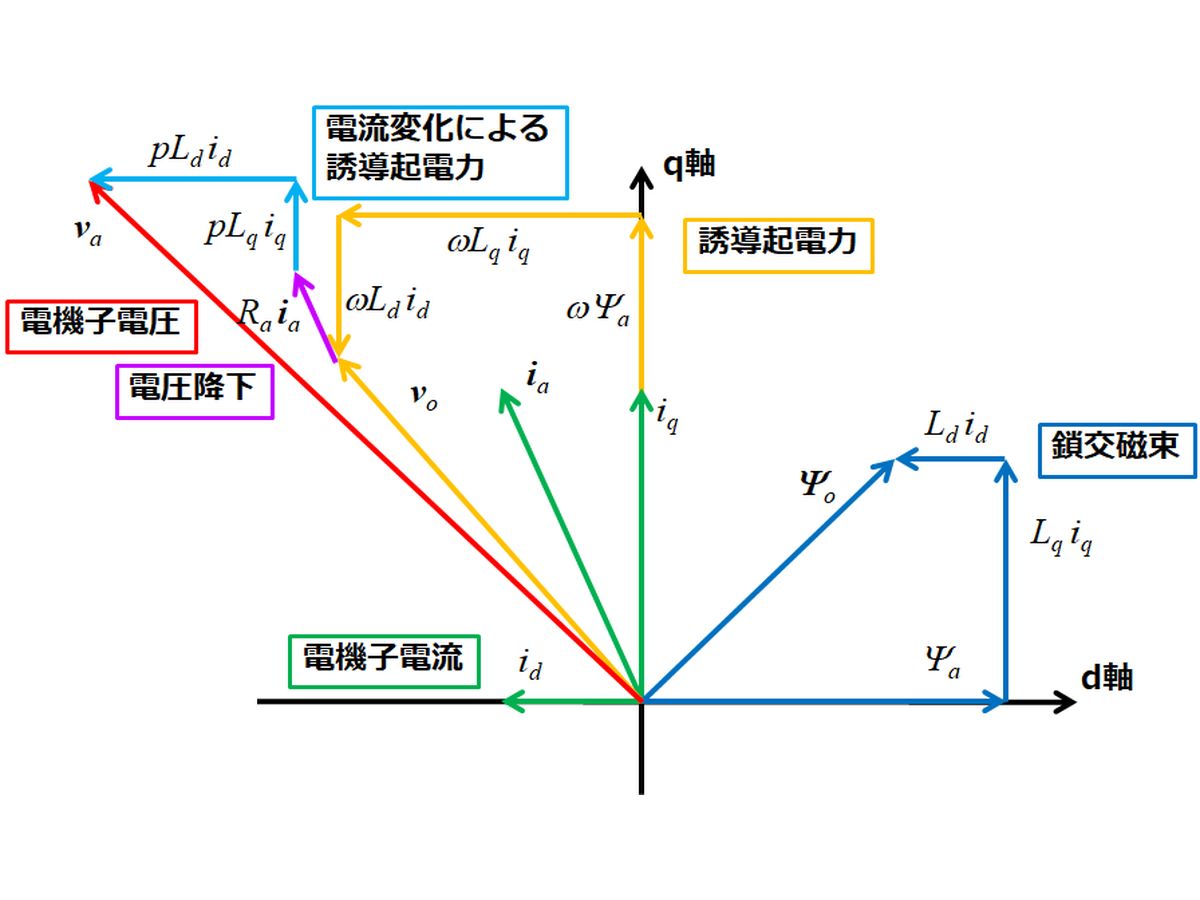
- d-q座標上の定常状態のベクトル図
- d-q座標上の鎖交磁束と誘導起電力の関係
- d-q座標上の非定常状態のベクトル図
質問・コメント等ございましたら，コメント欄，メールやTwitterよりご連絡ください。
