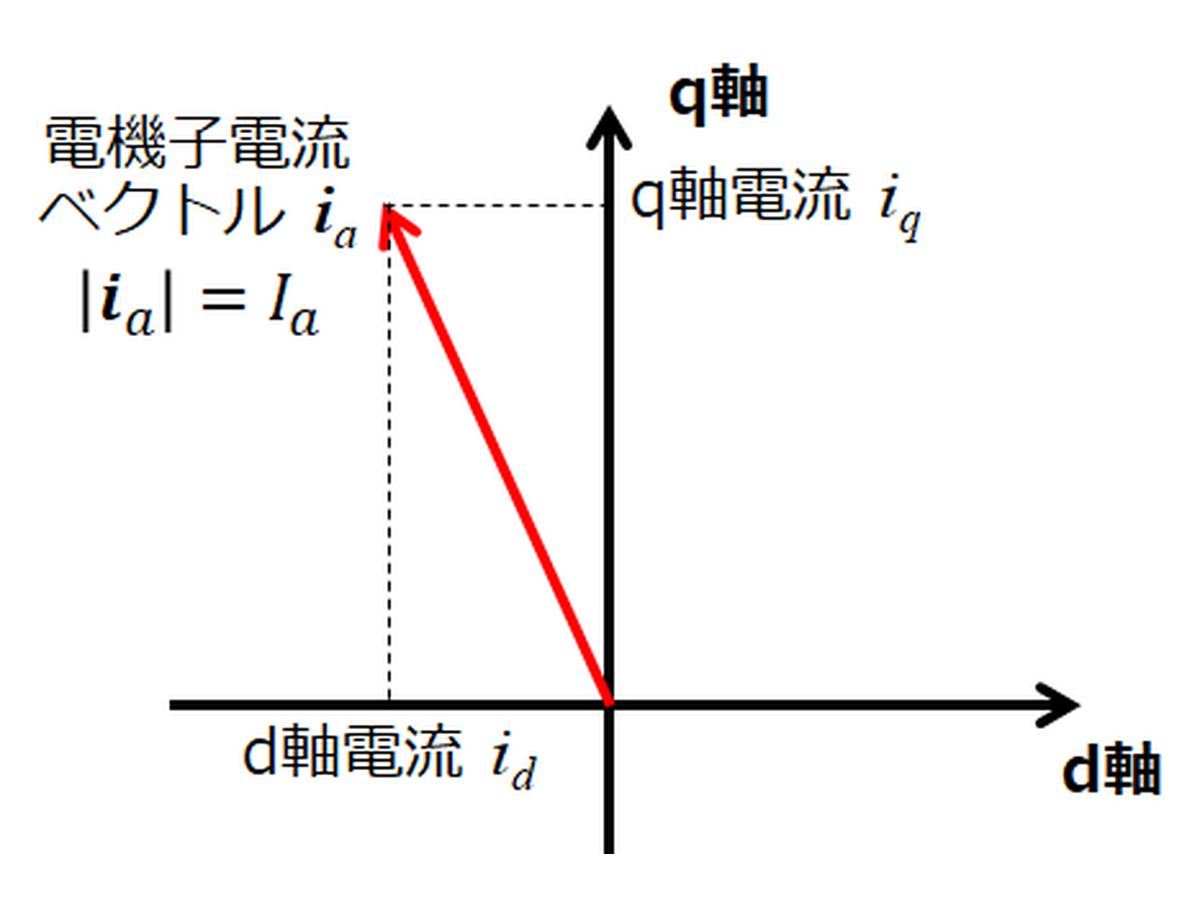
同期モータについて勉強したての頃は,電流だけで何種類も登場して混乱してしまう方も多いかと思います。私の場合,相電流と電機子電流の使い分けがうまくイメージできませんでした。特に,
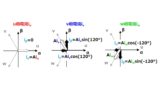
$$ I_a = \sqrt{3}I_e $$
この式はなんなんだ,と思っていました。($I_a$ は電機子電流ベクトルの大きさ,$I_e$ は相電流の実効値,絶対変換の場合)
上式で表される相電流実効値と電機子電流の関係は,実はそれぞれの銅損を考えるとイメージしやすくなります。本記事ではこのテーマについて説明していきます。
1. 言葉の定義
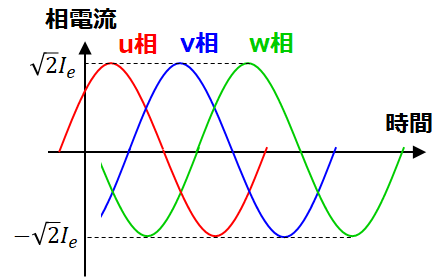
- 相電流:3相巻線に流れる平衡3相交流
- 電機子電流:3相交流電流を座標変換した電流
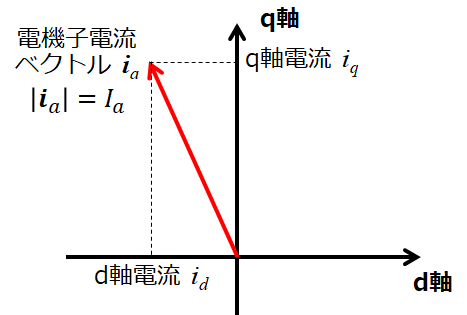
3相座標系からα-β座標系/d-q回転座標系に座標変換(絶対変換)した場合,相電流実効値と電機子電流の関係は次のように計算できます。(再掲)
$$ I_a = \sqrt{3}I_e $$
この式の座標変換を用いた導出は↓の記事を参考にしてください。
2. 相電流と電機子電流と銅損
まず,3相巻線を考えます。u相で発生する銅損 $W_u$ は,交流電流が流れていることから次のように計算できます。
$$ W_u = R_a I_e^2 $$
ここで,$R_a$ は1相あたりの巻線抵抗です。3相巻線に流れる電流は全て振幅が同じ(位相だけが違う)ため,各相で発生する銅損の値は等しく,モータ全体で発生する銅損 $W_c$ は各相の銅損を3倍したものになります。
$$ W_c = 3W_u =3R_a I_e^2 $$
次に,d-q回転座標系を考えます。(以下の議論はα-β座標上でも同様です。)d-q回転座標上では,回転子に同期して回転する仮想的なd,q相巻線を考えることができます。
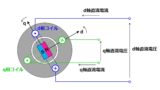
また,d,q相巻線の巻線抵抗はどちらもu,v,w相と同じであることが,電圧方程式からわかります。
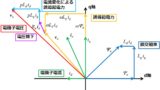
d,q相巻線には直流のd,q軸電流が流れているため,d,q相巻線で発生する銅損 $W_d,W_q$ およびモータ全体で発生する銅損 $W_c$ はそれぞれ次のように計算できます。
$$ W_d = R_a i_d^2 $$
$$ W_q = R_a i_q^2 $$
$$ W_c = W_d+W_q = R_a \left(i_d^2+i_q^2\right) = R_a I_a^2$$
先ほど導出した銅損の結果と比較すると,相電流と電機子電流の関係は次のように導出できます。
$$ W_c = 3R_a I_e^2 = R_a I_a^2$$
$$\Rightarrow\quad\sqrt{3}I_e = I_a$$
すなわち,相電流の $\sqrt{3}$ 倍の係数は,巻線が3相あることに起因する,と解釈することができます。
いかがでしょうか?
相電流から求める銅損は3相だから3倍する,電機子電流は全電流を統合したものなので1倍のまま,というイメージがあるだけでスッキリしませんか?
以上です。質問・コメント等ございましたら,コメント欄,メールやTwitterよりご連絡ください。
(今回は初学者向けのイメージの話なので,厳密な論理展開はしていません。ご了承ください。。。)
3. 参考文献
- 森本茂雄,真田雅之,省エネモータの原理と設計法,科学情報出版株式会社 (2013)