電気工学の分野で電圧波形や電流波形について検討するとき,フーリエ変換を用いて高調波を計算することが多いと思います。その時,交流回路の諸特性の高調波には奇数次高調波のみが発生し,偶数次高調波は全て0となっていることが多いです。
普段業務で扱っている方は慣れてしまっているかもしれませんが,そもそもなぜ奇数次高調波しか考えなくてよいのでしょうか?きちんと説明できますか?
本記事ではその数学的背景と直感的イメージについて説明します。
1. フーリエ変換のざっくり復習
周期 $2L$ の区分的になめらかな周期関数 $f(x)$ を考えると,そのフーリエ級数展開は
$$f(x)=\frac{a_{0}}{2}+\sum^{\infty}_{n=1}\left(a_{n}\cos \frac{n\pi x}{L}+b_{n} \sin \frac{n\pi x}{L}\right)$$
と表すことができます。ただし,フーリエ係数$a_{n}, b_{n}$は
$$a_{n}=\frac{1}{L}\int_{-L}^{L}f(u)\cos \frac{n\pi u}{L} \mathrm{d}u$$
$$b_{n}=\frac{1}{L}\int_{-L}^{L}f(u)\sin \frac{n\pi u}{L} \mathrm{d}u$$
です。
ここで,簡単のため $f(x)$ が奇関数である場合を考えます。(交流の特性を考えるので,適当な時間を初期値とすれば奇関数とみなせます。)
このとき,$\cos \frac{n\pi u}{L}$ は偶関数であることから $f(u)\cos \frac{n\pi u}{L}$ は奇関数となり,
$$a_{n}=\frac{1}{L}\int_{-L}^{L}f(u)\cos \frac{n\pi u}{L} \mathrm{d}u=0$$
と計算できます。よって,以下では
$$f(x)=\sum^{\infty}_{n=1}b_{n}\sin \frac{n\pi x}{L}$$
として考えます。
2. 半波対称性と奇数次高調波の関係
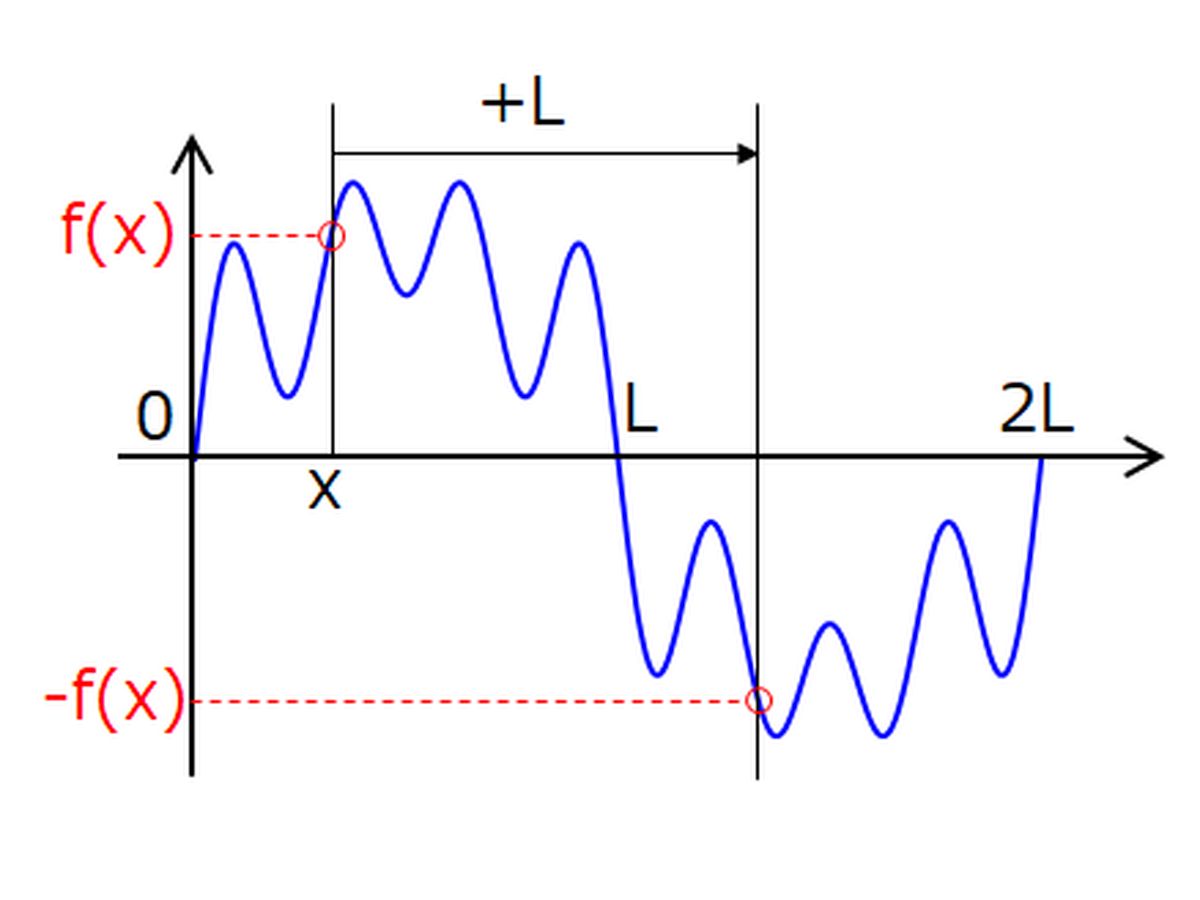
結論からいうと,偶数次高調波を無視できる理由は半波対称性です。
半波対称性とは,次式の関係が常に成り立つ性質のことです。
$$f(x)=-f(x+L)$$
図にするとこんな感じ。
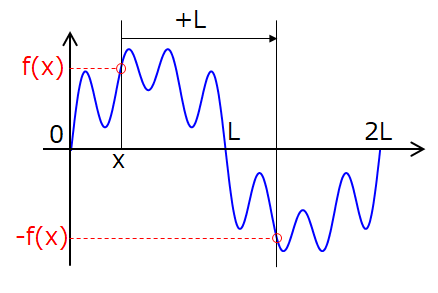
ちょうど半周期ごとに同じ波形が上下対称に出現するイメージですね。
それでは,半波対称性を持つ関数が奇数次高調波しか持たないことを,フーリエ係数に着目して証明します。
(証明)
$$f(x)=\sum^{\infty}_{n=1}b_{n}\sin \frac{n\pi x}{L}$$
$$\begin{eqnarray}
-f(x+L)&=&-\sum^{\infty}_{n=1}b_{n}\sin \frac{n\pi}{L}\left(x+L\right) \\
&=&-\sum^{\infty}_{n=1}b_{n}\sin \left(\frac{n\pi x}{L}+n\pi\right) \\
&=&\begin{cases}
-\sum^{\infty}_{n=1}b_{n}\sin \left(\frac{n\pi x}{L}\right) (n: 偶数の場合) \\
\sum^{\infty}_{n=1}b_{n}\sin \left(\frac{n\pi x}{L}\right) (n: 奇数の場合)
\end{cases}\end{eqnarray}$$
であるから,$f(x)=-f(x+L)$が成立するためには,$n$ が偶数の時 $b_{n}=0$ であることが必要十分である。
3. 奇数次高調波のみを考慮する直感的な解釈
フーリエ係数を計算することで,半波対称性を持つ関数が偶数次高調波を持たないことを証明できました。この事実は高調波成分の波形をイメージすると理解しやすくなります。
フーリエ変換では,下図のような複数の正弦波の重ね合わせとして関数を解釈しています。
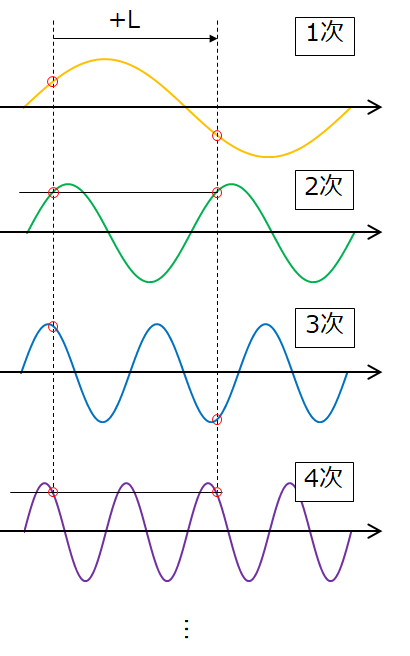
それぞれの正弦波に着目すると,奇数次の正弦波は半波対称性を示しますが,偶数次の正弦波は半波対称性を示しません。そのため,偶数次の正弦波の振幅がゼロでなければ,その重ね合わせの関数が半波対称性を示さなくなってしまいます。だから,半波対称性を有する関数では奇数次高調波成分のみを考えています。
以上です。質問・コメント等ございましたら,問い合わせフォームや下部のコメント欄,メールやTwitterよりご連絡ください。
4. 参考文献
- 小郷 寛,石亀篤司,小亀英己,基礎からの交流理論,電気学会 (2002)