dq回転座標系に6n次高調波が発生する直感的な解釈

同期モータでは、振動や騒音といった特性が一つの重要課題となっています。これらの特性の主要因の一つが、電流や磁束の高調波です。本記事では、dq回転座標系において6の倍数次高調波が発生する直感的な解釈について説明します。

関連する計算は↓で行っているので、この記事では複雑な数式は扱いません。

トルクリプルが6の倍数次高調波として現れる理由

同期モータのトルクリプルは主に6の倍数次高調波として出現します。本記事は、電機子鎖交磁束の奇数次高調波がトルクの6の倍数次高調波として出現する数学的な理由について説明します。そもそもなぜ奇数次高調波のみで良いのかはこちらをどうぞ↓ ...

1. 問題の定義
2. 直感的な解釈
3. まとめ
4. 参考文献

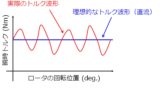
1. 問題の定義

平衡3相交流で駆動する同期モータを考えます。以下では鎖交磁束をベースに話を進めていきますが、物理量は電流でも電圧でもなんでも構いません。

電機子鎖交磁束の基本波を次式で定義します。初期位相や相順などを変えても議論は成立します。

$$
\begin{matrix}
\varPsi_{u1} = \varPsi_1 \cos \left( \omega t \right) \quad \; \; \; \; \; \; \\
\varPsi_{v1} = \varPsi_1 \cos \left( \omega t + \frac{2 \pi }{3} \right) \\
\varPsi_{w1} = \varPsi_1 \cos \left( \omega t \; – \; \frac{2 \pi }{3} \right)\;\\
\end{matrix}
$$

ここで、$\varPsi_{xh}$ は h 次成分の x 相の電機子鎖交磁束、$\varPsi_1$ は振幅、$ \omega $ は角速度です。

鎖交磁束に発生する高調波は、半波対称性より奇数次のみです。

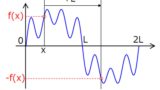
なんで交流回路では奇数次高調波しか考えなくて良いんですか？ー半波対称性とフーリエ変換ー

電気工学の分野で電圧波形や電流波形について検討するとき，フーリエ変換を用いて高調波を計算することが多いと思います。その時，交流回路の諸特性の高調波には奇数次高調波のみが発生し，偶数次高調波は全て0となっていることが多いです。普段業務...

また、3相座標⇒αβ座標の変換の途中で、3n 次高調波（n：自然数）は消えてしまいます。（↓記事スライドの p.6）

トルクリプルが6の倍数次高調波として現れる理由

よって、本記事で考えるべき3相座標系の高調波次数 $h$ は、
$$h=5, 7, 11, 13, 17, 19,…=6n \pm 1$$
です。↑の記事で、これらの高調波次数成分を座標変換すると、確かに dq 軸上で 6n 次高調波となることは確認済みです。本記事では、これらの直感的な解釈を考えます。

2. 直感的な解釈

$h$ 次の高調波磁束は次式の通りです。初期位相は簡単のため記載していません。（考慮しても同じ結果です。）

$$
\begin{matrix}
\varPsi_{uh} = \varPsi_h \cos \left( h \omega t \right) \quad \; \; \; \; \; \; \; \; \; \\
\varPsi_{vh} = \varPsi_h \cos \left( h \left( \omega t + \frac{2 \pi }{3} \right) \right) \\
\varPsi_{wh} = \varPsi_h \cos \left( h \left( \omega t \; – \; \frac{2 \pi }{3} \right) \right)\;\\
\end{matrix}
$$

よって $h=6n+1=7, 13, 19…$ の場合、高調波磁束は以下のように計算できます。

$$
\begin{matrix}
\varPsi_{u6n+1} = \varPsi_{6n+1} \cos \left( \left( 6n+1 \right) \omega t \right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \; \; \; \; \; \; \; \; \; \; \; \; \; \; \\
\varPsi_{v6n+1} = \varPsi_{6n+1} \cos \left( \left( 6n+1 \right) \omega t + 4n \pi + \frac{2 \pi }{3} \right) = \varPsi_{6n+1} \cos \left( \left( 6n+1 \right) \omega t+ \frac{2 \pi }{3} \right) \\
\varPsi_{w6n+1} = \varPsi_{6n+1} \cos \left( \left( 6n+1 \right) \omega t \; – \; 4n \pi \; – \; \frac{2 \pi }{3} \right) = \varPsi_{6n+1} \cos \left( \left( 6n+1 \right) \omega t \; – \; \frac{2 \pi }{3} \right) \; \; \\
\end{matrix}
$$

また、$h=6n \; – \; 1=5, 11, 17…$ の場合は以下の通りです。

$$
\begin{matrix}
\varPsi_{u6n-1} = \varPsi_{6n-1} \cos \left( \left( 6n \; – \;1 \right) \omega t \right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \; \; \; \; \; \; \; \; \; \; \; \; \; \\
\varPsi_{v6n-1} = \varPsi_{6n-1} \cos \left( \left( 6n \; – \;1 \right) \omega t + 4n \pi \; – \; \frac{2 \pi }{3} \right) = \varPsi_{6n-1} \cos \left( \left( 6n \; – \;1 \right) \omega t \; – \; \frac{2 \pi }{3} \right) \;\\
\varPsi_{w6n-1} = \varPsi_{6n-1} \cos \left( \left( 6n \; – \;1 \right) \omega t \; – \; 4n \pi + \frac{2 \pi }{3} \right) = \varPsi_{6n-1} \cos \left( \left( 6n \; – \;1 \right) \omega t + \frac{2 \pi }{3} \right)\\
\end{matrix}
$$

これらを比較すると、$h=6n \; – \; 1$ の場合は v 相と w 相の位相が逆になっています。すなわち、回転磁界の回転方向に関して、$6n + 1$ 次の高調波成分は基本波と同じ方向に回転するのに対し、$6n \; – \; 1$ 次の高調波成分は逆転します。またその回転角速度は、$6n + 1$ 次成分は $(6n + 1)\omega$、$6n \; – \; 1$ 次成分では$(6n \; – \; 1)\omega$ です。

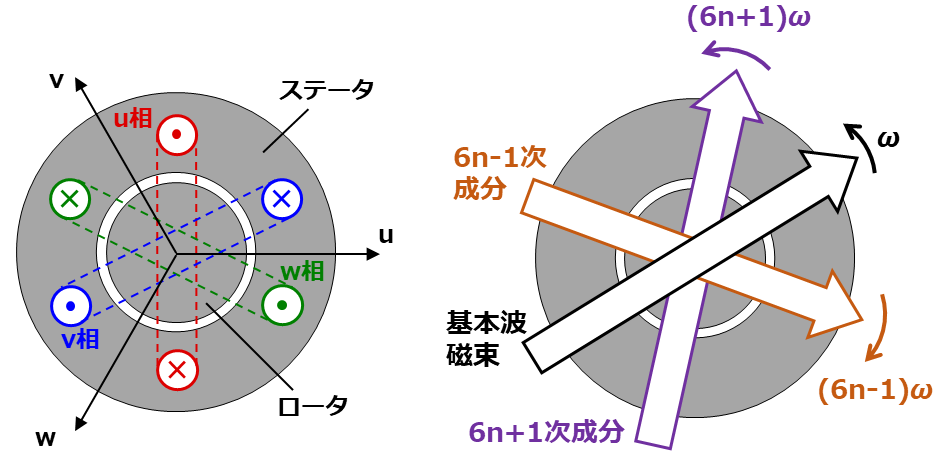
そして、dq軸は回転磁界の基本波成分に同期して角速度 $\omega$ で回転する座標系です。

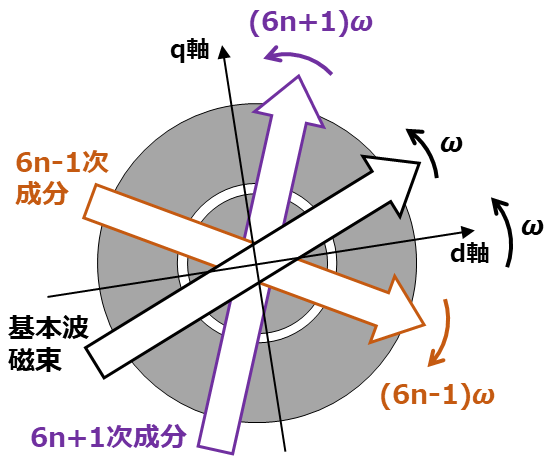
そのため、dq軸から見た回転磁界の高調波成分の相対速度は、それぞれ次のようになります。

$$
\begin{matrix}
\left( 6n+1 \right) \omega \; – \; \omega = 6n \omega \\
– \; \left( 6n \; – \; 1 \right) \omega \; – \; \omega = – \; 6n \omega \\
\end{matrix}
$$

以上より、3相座標系での $6n \pm 1$ 次高調波が、dq回転座標系では全て $6n$ 次となることがわかりました。

3. まとめ

3相座標系で発生する高調波のうち、 $6n + 1$ 次成分は $(6n + 1)\omega$ の角速度でロータと同じ方向に回転し、$6n \; – \; 1$ 次成分は $(6n \; – \; 1)\omega$ の角速度で逆転します。これらを角速度 $\omega$ のdq回転座標系から見ると、どちらも $6n$ 次の角速度（すなわち周波数成分）に見えるという訳ですね。なんとなく高調波のイメージが付きましたか？