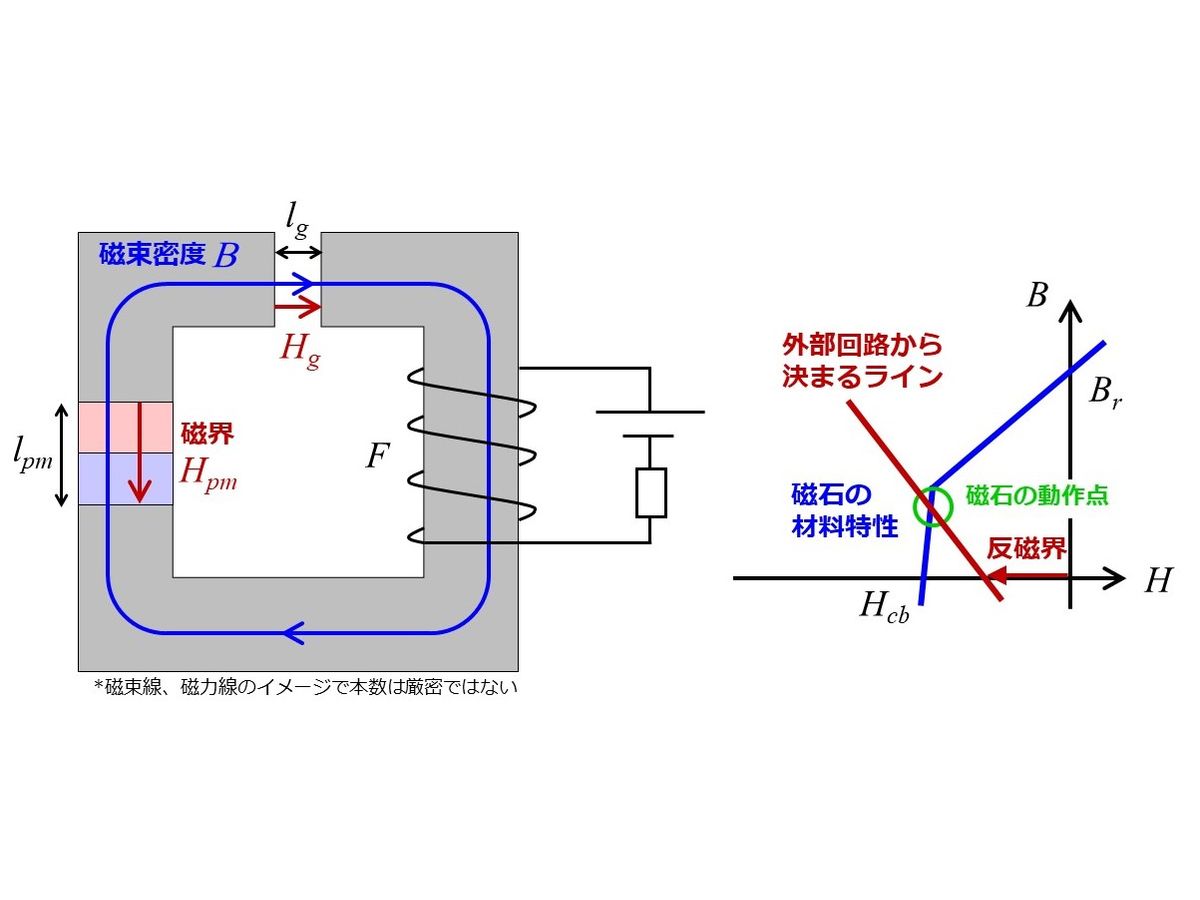
永久磁石は磁石同期モータの重要な構成部品の一つです。永久磁石の特性の一つにはB-Hカーブがありますが、モータ駆動中の動作点は主に磁界が負の領域(特に第2象限)です。本記事では、モータ駆動時の磁石動作点の磁界が負となる理由について解説します。
*想定読者はモータ技術者なので、磁性体の物理的背景などをすっ飛ばして書いています
1. 本記事で考える永久磁石
永久磁石のB-Hカーブの代表例を下図に示します。
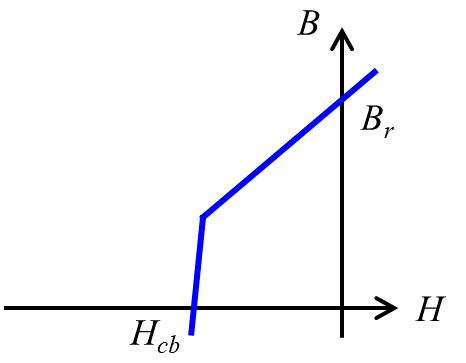
ここで、$B$ は磁束密度、$H$ は磁界、$B_r$ は残留磁束密度(縦軸との交点)、$H_{cb}$ は保磁力(横軸との交点;実際はもう一種あるが割愛)です。一般に、永久磁石はB-Hカーブの第2,3象限で非線形に変化する(不可逆減磁する)点をもちます。
2. 単純な磁気回路から考えてみる
2.1 ロの字鉄心とコイル
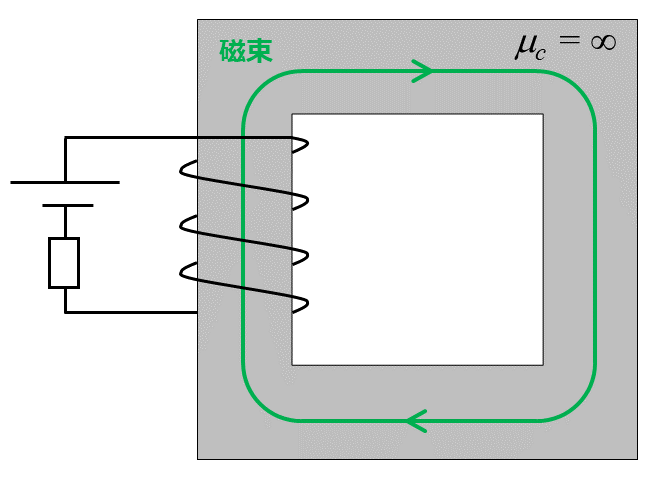
まずは単純なコイルの磁気回路を考えます。簡単のため、コアの透磁率 $\mu_c$ を無限大と仮定し、また漏れ磁束は無視しています。図のようにロの字型の鉄心にコイルが巻いてある場合、等価磁気回路は次のようになります。
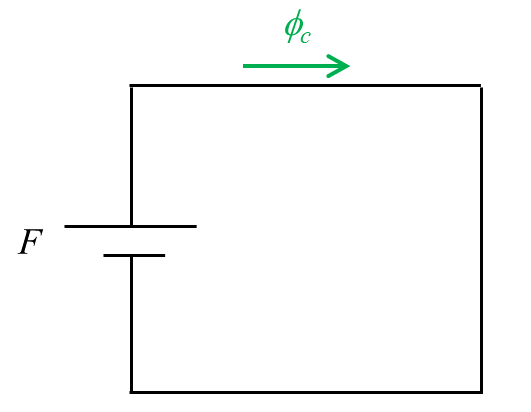
ここで、$F$ はコイルの起磁力、$\phi_c$ は磁束であり、コアの透磁率が無限大のため回路の磁気抵抗 $R_c$ は 0 A/Wb です。
磁気回路におけるオームの法則から、磁束は無限大となります。
$$ \phi_c = \frac{F}{R_c} ~ \infty $$
2.2 コの字鉄心とコイル
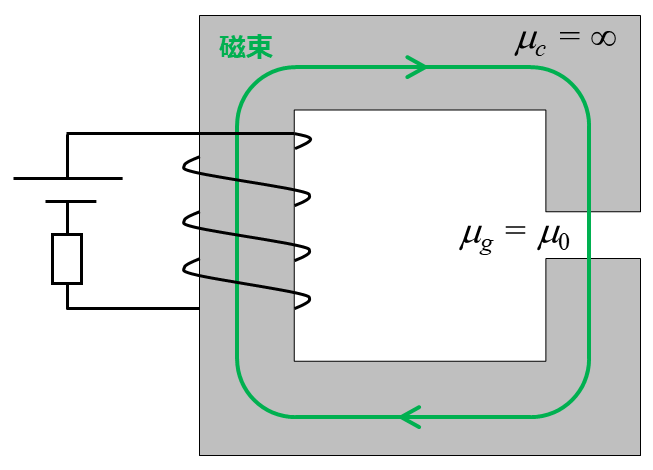
続いて、図のようにギャップの存在するコの字型の鉄心にコイルが巻いてある場合を考えます。ギャップ部の透磁率 $\mu_g$ は真空の透磁率 $\mu_0$ とします。等価磁気回路は次のようになります。
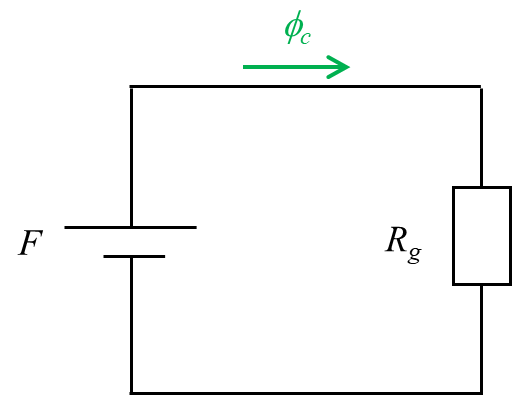
ここで、$R_g$ はギャップ部の磁気抵抗です。さきほどと同様にオームの法則から、以下の関係が成り立ちます。
$$ \phi_c = \frac{F}{R_g} $$
2.3 コの字鉄心と永久磁石
2.3.1 永久磁石の磁束密度と磁界
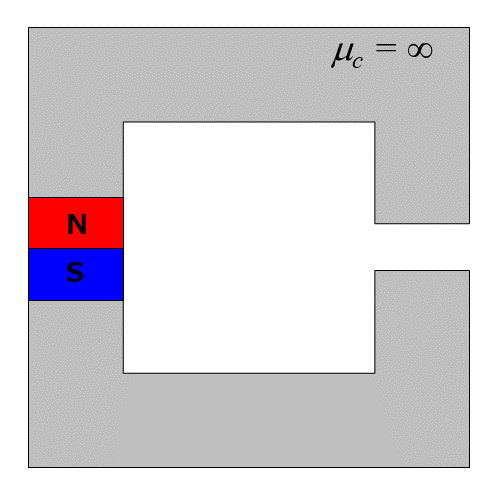
ここからが本番です。永久磁石がコの字型の鉄心に組み込まれている状態を考えます。磁気回路を考えたいですが、永久磁石をどう表現すべきかわかりません。
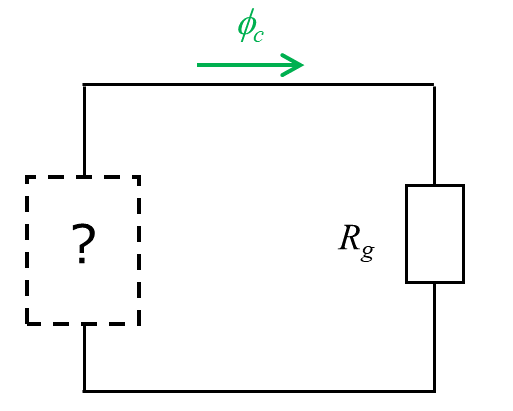
そこで、電磁気の世界まで立ち返って、磁束密度と磁界の状態を考えましょう。まず、異なる磁性体の境界において、境界面近傍でのガウスの法則より、磁束密度の法線成分は等しくなるのでした。磁気回路法では基本的に法線方向しか考えないので、永久磁石内とコア内、ギャップ内で磁束密度は等しいことがわかります。
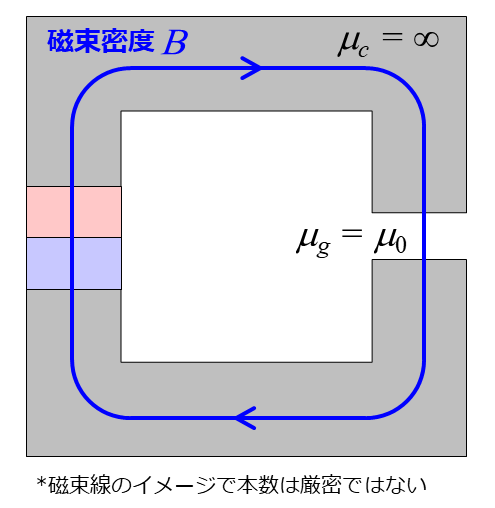
他方、異なる磁性体の境界において、磁界の法線成分は必ずしも等しいとは限りません。そこで、磁束密度から磁界の強さを計算をします。コア、ギャップ部の磁界 $H_c, H_g$ はそれぞれ、次のように計算できます。
$$
\begin{matrix}
H_c = \frac{B}{\mu_c} \sim 0 \\
H_g = \frac{B}{\mu_g} = \frac{B}{\mu_0} \\
\end{matrix}
$$
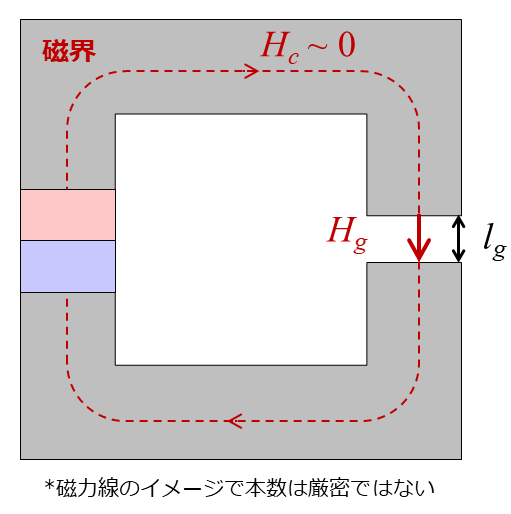
磁界の強さは単位長さ当たりの起磁力なので、ギャップ部の長さを $l_g$ とすると、ギャップ部の起磁力 $F_g$ は以下のように計算できます。
$$ F_g = l_g H_g = \frac{l_g B}{\mu_0} $$
また、電流が0の時のアンペールの法則(もしくは磁気回路におけるキルヒホッフの法則)より、ギャップ部の起磁力 $F_g$ と永久磁石部の起磁力 $F_{pm}$ には以下の関係が成り立ちます。
$$ F_g + F_{pm} = 0 $$
以上より、永久磁石の長さを $l_{pm}$ とすると、永久磁石の磁界 $H_{pm}$ は次式のように求まります。
$$ H_{pm} = \frac{F_{pm}}{l_{pm}} = \frac{- F_g}{l_{pm}} = -\frac{l_g}{\mu_0 l_{pm}}B_{pm} $$
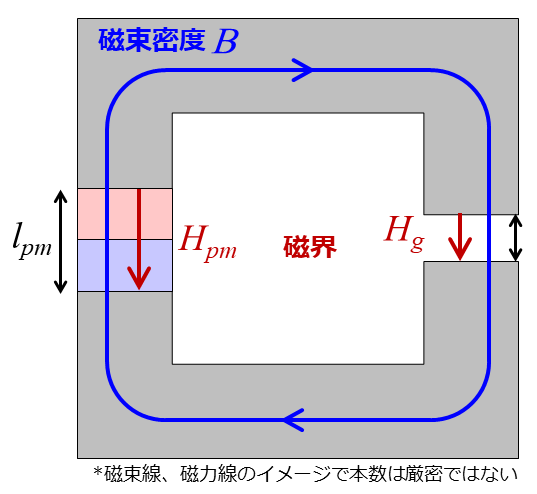
したがって、永久磁石には磁束密度とは逆方向の磁界が発生していることがわかります。これこそが、永久磁石の動作点磁界が負となる理由です。
2.3.2 永久磁石の動作点
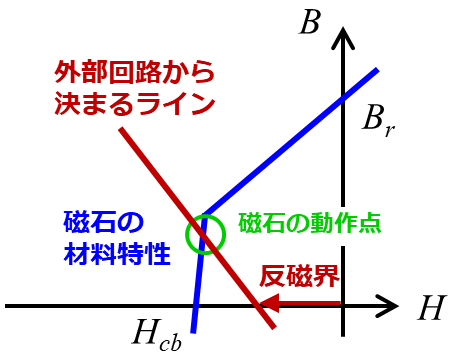
もう少し理解を深めるために、実際の磁石動作点を求める方法について述べておきましょう。動作点を求めるのは非常に簡単で、2.3.1項の最終式とB-Hカーブの交点を求めるだけです。
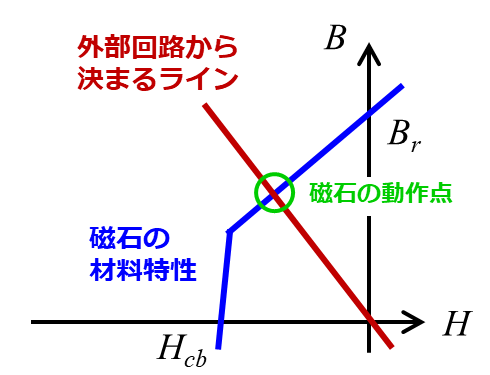
2.3.1項では永久磁石の特性には全く言及しておらず、その他の物理的な関係のみから議論を進めていました。すなわち、2.3.1項の最終式は磁石も含めた外部の回路状態から求まる直線であり、それと永久磁石が本来有する材料特性とが釣り合う点として、磁石の動作点が決まっています。
2.4 ロの字鉄心と永久磁石
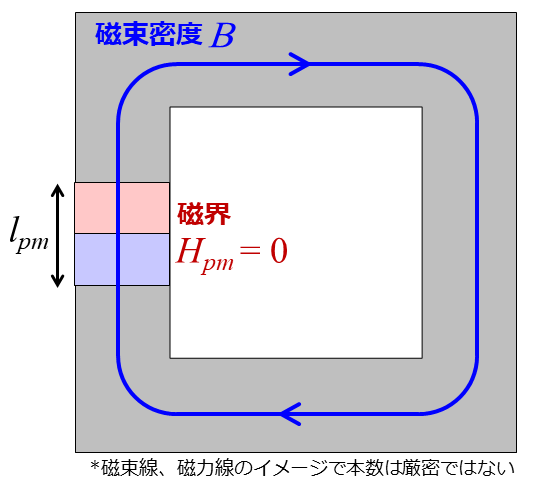
なんとなく理解したところで、もう少し別の簡単な例を見ていきましょう。ギャップがない磁気回路です。
2.3.1項と同様に、電流が0の時のアンペールの法則(もしくは磁気回路におけるキルヒホッフの法則)より、永久磁石の起磁力と磁界の強さは0となります。
$$ F_{pm} = 0, H_{pm} = 0 $$
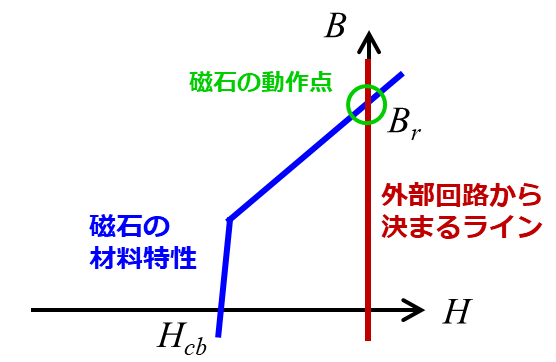
したがって、磁石の動作点は $(H, B) = (0, B_r)$ と求まります。
2.5 コイルの巻かれたロの字鉄心と永久磁石
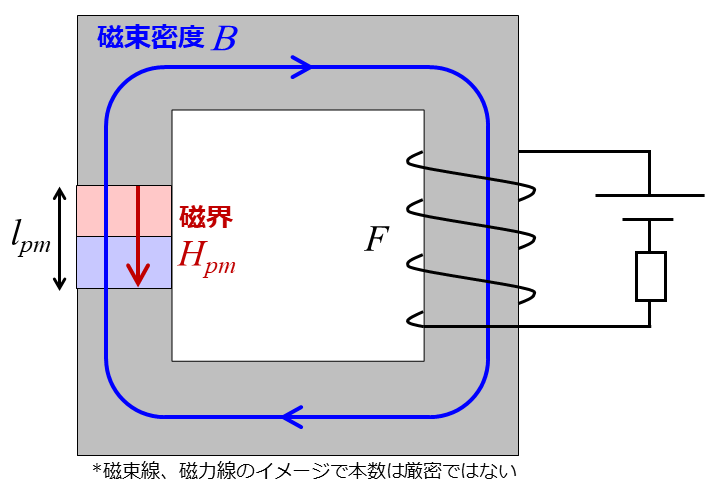
続いて、永久磁石とコイルが両方存在する磁気回路を考えます。コイルの向きは永久磁石にとって反磁界が発生する方向とし、実際のモータ駆動時の状態に近づけていきます。
電流が0の時のアンペールの法則(もしくは磁気回路におけるキルヒホッフの法則)より、永久磁石の起磁力とコイルの起磁力の合計は0となります。
$$ F_{pm}+F = 0 $$
したがって、永久磁石の磁界は次のように計算できます。
$$ H_{pm} = \frac{F_{pm}}{l_{pm}} = \frac{-F}{l_{pm}} $$
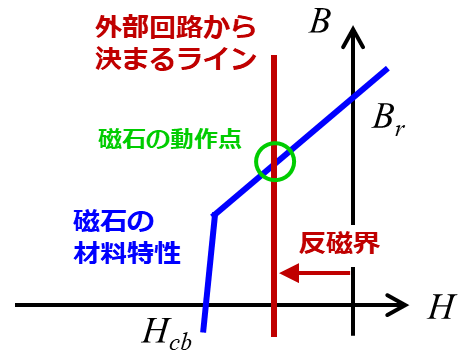
回路上にコイルが存在する場合、外部回路から決まるラインが原点から移動することがわかります。
2.6 コイルの巻かれたコの字鉄心と永久磁石
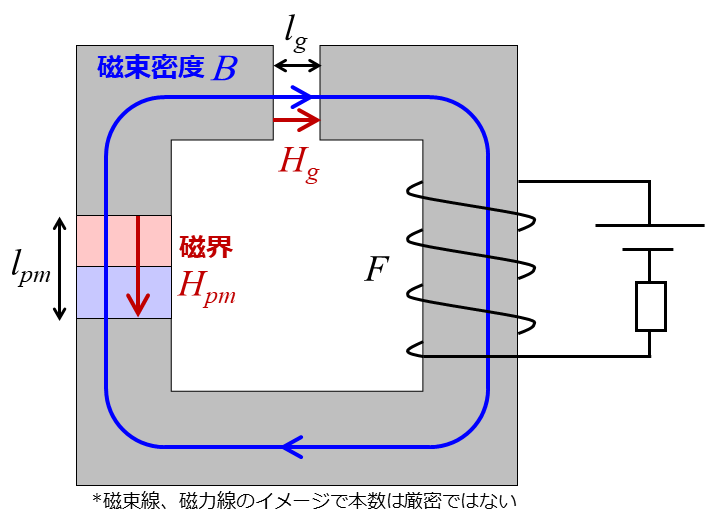
最後に永久磁石とコイル、ギャップ部がすべて存在する磁気回路を考えます。先ほどと同様に、コイルの向きは永久磁石にとって反磁界が発生する方向とします。最も単純化されたモータの磁気回路状態です。
まず、2.3.1項と同様にして、永久磁石とコア、ギャップ部の磁束密度はすべて同じであることがわかります。また、ギャップ部の起磁力は次式のように計算できます。
$$ F_g = l_g H_g = \frac{l_g B}{\mu_0} $$
永久磁石、ギャップ部、コイルの起磁力の合計は0です。
$$ F_{pm}+F_g+F = 0 $$
したがって、永久磁石の磁界は次のように計算できます。
$$
\begin{matrix}
F_{pm} = -F_g-F \\
H_{pm} = \frac{F_{pm}}{l_{pm}} = \frac{- F_g-F}{l_{pm}} = -\frac{l_g}{\mu_0 l_{pm}}B_{pm} – \frac{F}{l_{pm}} \\
\end{matrix}
$$
コイルがない磁気回路で求まる直線を、コイルの起磁力分だけ平行移動した結果となりました。
3. 永久磁石の等価回路
最後に、2章の結果から、永久磁石の磁気回路上の等価回路を求めておきます。永久磁石は、内部抵抗を有する起磁力源もしくは磁束源としてあらわされます。(電池のようなイメージ)
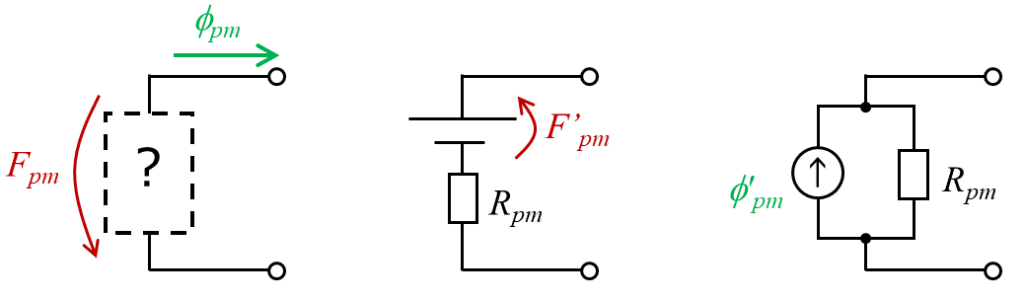
図の $F_{pm}$ の向きに違和感を覚えるかもしれませんが、外部から見たインピーダンスを考えると、磁束の向きに対して起磁力が逆向きであるのは当然です。
磁石の磁気抵抗 $R_{pm}$ は、磁石の透磁率を真空の透磁率と同じと仮定して、次式で求めることが多いです。ただし、$S_{pm}$ は磁石の断面積です。
$$ R_{pm} = \frac{l_{pm}}{\mu_0 S_{pm}}$$
磁石の起磁力源 $F’_{pm}$ や磁束源 $\phi’_{pm}$ は、2.4節のような短絡回路を考えると導出できます。2.4節の磁石動作点の検討結果から、回路短絡時の磁束は次のように求まります。
$$ \phi_{pm} = S_{pm} B_r$$
まず、起磁力表現の等価回路に関しては、起磁力源と内部抵抗にかかる起磁力は等しくなるので、以下のように計算できます。
$$ F’_{pm} = R_{pm} \phi_{pm} = R_{pm} S_{pm} B_r = \frac{l_{pm}}{\mu_0} B_r $$
磁束表現の等価回路に関しては、内部抵抗に流れる磁束が0になるので、以下のように計算できます。
$$ \phi’_{pm} = \phi_{pm} = S_{pm} B_r $$
4. まとめ
本記事では、パーミアンス法の基礎的な部分を解説しました。磁石動作点が第二象限となる理由は、永久磁石の磁束密度と磁界の向きが逆になるという、直感に反する事象が要因でした。最近は有限要素解析が発達し短時間で高精度な解が得られるようになりましたが、パーミアンス法ベースで定性的に特性を理解することも重要なので、考え方をきちんと理解しておきましょう。
5. 参考文献
[1] A. E. Fitzgerald, Charles Kingsley, Jr., and Stephen D. Umans, “Electric Machinery,” McGraw-Hill (6th edition), 2005.
以上です。質問・コメント等ございましたら、メールやTwitterよりご連絡ください。