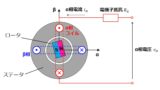
磁石同期モータ(PMSM: Permanent Magnet Synchronous Motor)の業務をしていると、目の前にあるモータのインダクタンスがどれくらいか測定したくなる時があります。しかし、3相の電圧と電流を測定して電圧方程式から計算…というのは少々煩雑です。そこで、より簡単な方法として、LCRメータを用いてPMSMのインダクタンスを測定する方法について、本記事では紹介したいと思います。
インダクタンスってそもそも何なんだ、という方はこちら↓。
1. インダクタンスの定式化
まず、インダクタンスを定式化します。

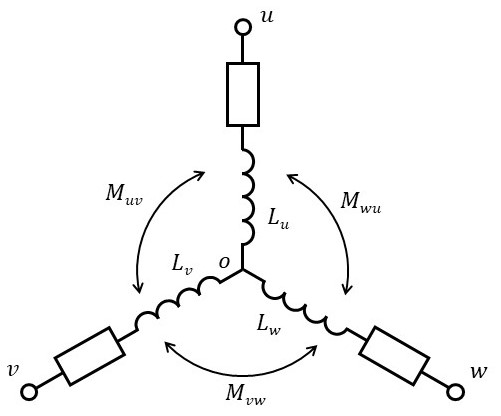
↑の記事では、PMSMのuvw相自己インダクタンスと各相間の相互インダクタンスは次式で与えました。ここで、ステータ巻線はスター結線を想定します。
$$
\begin{matrix}
L_u = l_a + L_a – L_{as} \cos \left( 2 \theta \right) \quad \; \; \; \; \; \; \\
L_v = l_a + L_a – L_{as} \cos \left( 2 \theta + \frac{2 \pi }{3} \right) \\
L_w = l_a + L_a – L_{as} \cos \left( 2 \theta – \frac{2 \pi }{3} \right) \; \; \; \\
\end{matrix}
$$ $$
\begin{matrix}
M_{uv} = M_{vu} = -\frac{1}{2} L_a – L_{as} \cos \left( 2 \theta – \frac{2 \pi }{3} \right) \; \; \; \\
M_{vw} = M_{wv} = -\frac{1}{2} L_a – L_{as} \cos \left( 2 \theta \right) \quad \; \; \; \; \; \; \\
M_{wu} = M_{uw} = -\frac{1}{2} L_a – L_{as} \cos \left( 2 \theta + \frac{2 \pi }{3} \right) \\
\end{matrix}
$$
ここで、$L_x$ は x 相の自己インダクタンス、$M_{xy}$ は x,y 相間の相互インダクタンス、$l_a$ は漏れインダクタンス、$L_a$ は有効インダクタンスの平均値、$L_{as}$ は有効インダクタンスの基本波振幅、$\theta$ は回転角です。
また、座標変換した後のインダクタンスの値が知りたい場合もあります。
↑の記事から、d, q軸インダクタンスは次式の通りです。
$$
\begin{matrix}
L_d = l_a + \frac{3}{2} L_a – \frac{3}{2} L_{as}\; \; \;\\
L_q = l_a + \frac{3}{2} L_a + \frac{3}{2} L_{as}\\
\end{matrix}
$$
後の計算のため、3相電圧方程式も導入しておきます。
$$
\begin{pmatrix}
v_u \\
v_v \\
v_w \\
\end{pmatrix} = R_a \\
\begin{pmatrix}
i_u \\
i_v \\
i_w \\
\end{pmatrix} + \frac{d}{dt} \\
\begin{pmatrix}
L_u & M_{uv} & M_{wu} \\
M_{uv} & L_v & M_{vw} \\
M_{wu} & M_{vw} & L_w \\
\end{pmatrix} \\
\begin{pmatrix}
i_u \\
i_v \\
i_w \\
\end{pmatrix} + \frac{d}{dt} \\
\begin{pmatrix}
e_{u} \\
e_{v} \\
e_{w} \\
\end{pmatrix}
$$
ここで、$R_a$ は巻線抵抗、$e_x$ は x 相の界磁磁束による誘起電圧です。詳細はこちら↓
2. LCRメータによる計測
それでは、LCRメータを用いてインダクタンスを計測する方法について説明します。用意するものは測定対象のモータとLCRメータのみです。
2.1 中性点が引き出せない場合
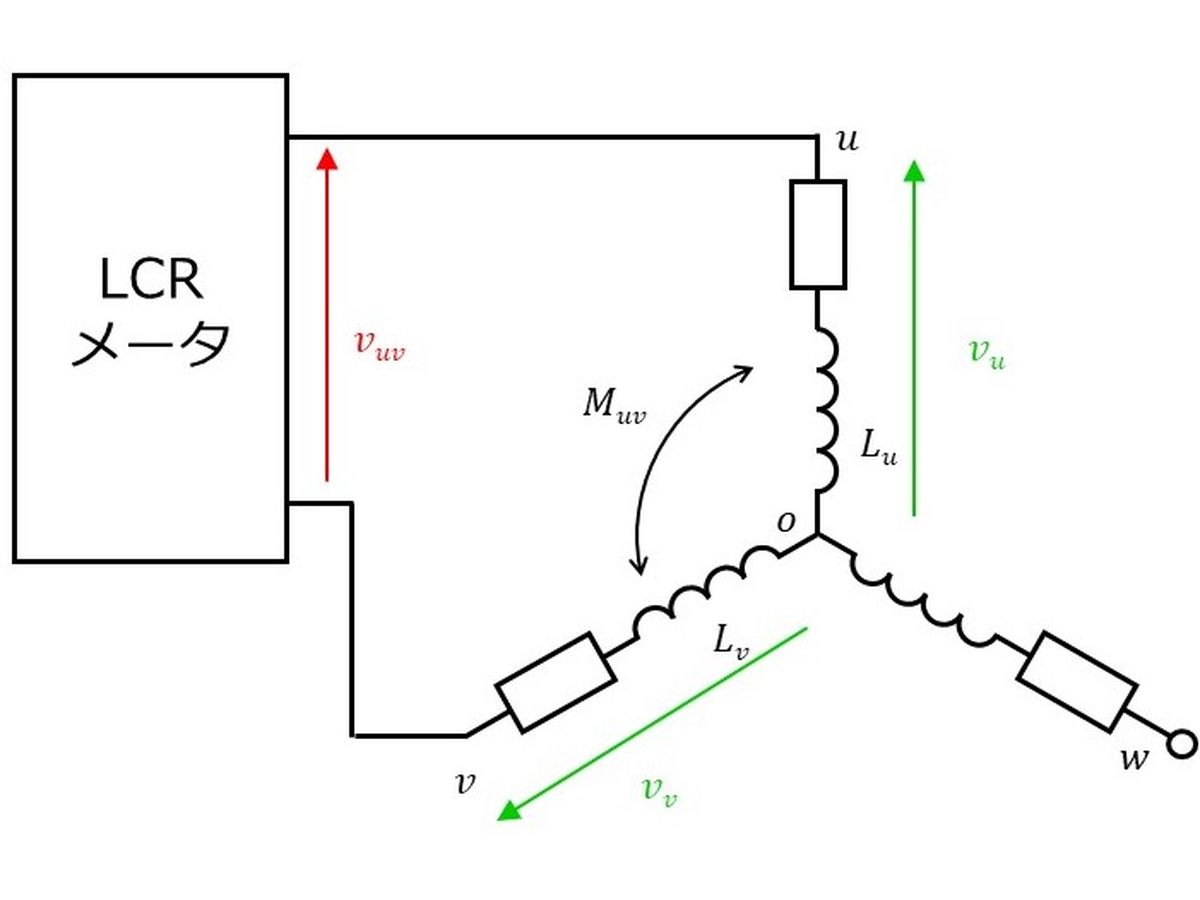
最も単純な方法は、u-v間など、任意の2相間にLCRメータを繋いで測定する方法です。
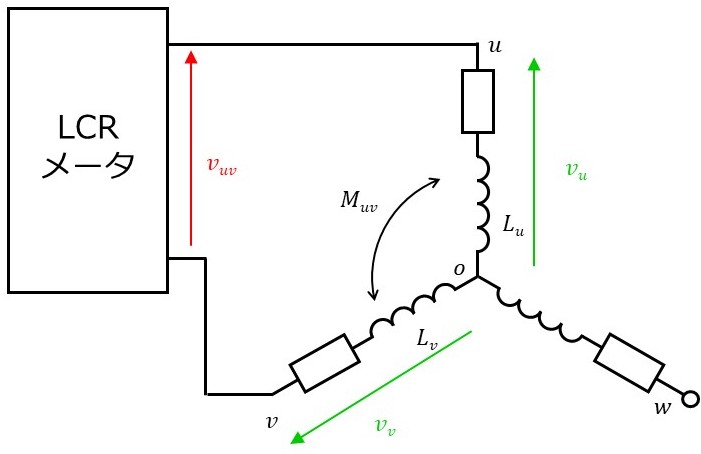
この場合、LCRメータにより測定できるインダクタンスには、u,v相の自己インダクタンスとu-v相間の相互インダクタンスが含まれます。ここで、u-v相間の電圧方程式を導出すれば、測定するインダクタンスの正体が明らかになります。
u,v相の電流は、それぞれ振幅が同じで正負が異なるので $i_u = I, i_v = -I$ とし、接続されていないw相電流は $i_w = 0 \rm{A}$ とします。静止状態を考えるので誘起電圧 $e_u = e_v = e_w = 0 \rm{V}$ とすると、u-v相間電圧 $v_{uv}$ は次式のように計算できます。
$$ v_{uv} = v_u – v_v = \frac{d}{dt} \left( L_u – M_{uv} – M_{uv} + L_v \right) I $$
したがって、LCRメータで計測できるインダクタンス成分 $L_{lcr}$ は次式のように求まります。
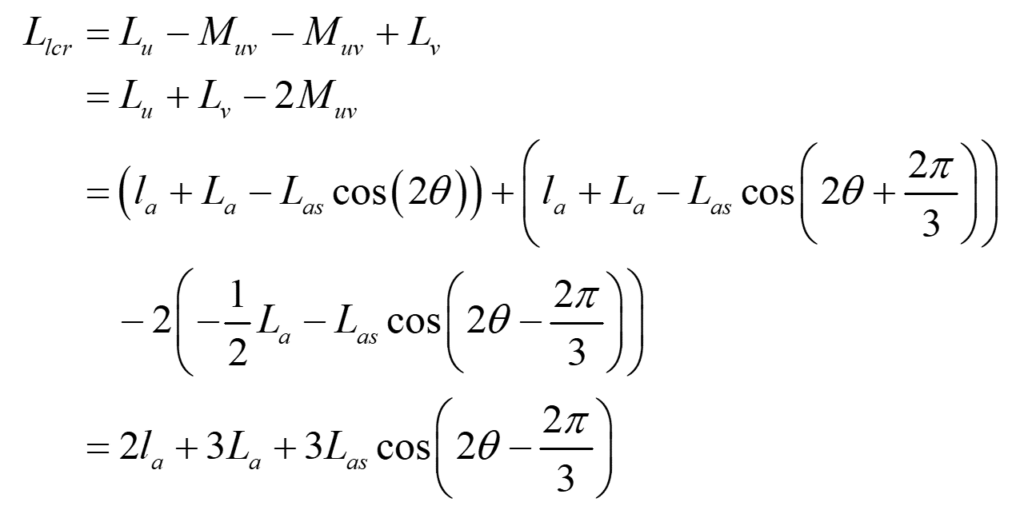
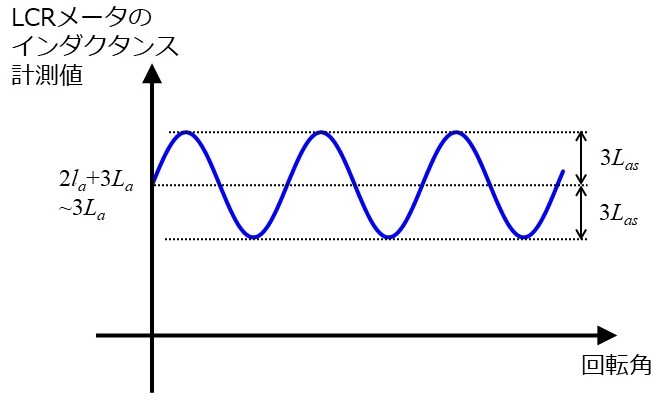
実際の計測では、回転子位置を変えながらインダクタンスを測定します。測定結果は上図のようなサインカーブとなり、この結果からパラメータ $l_a, L_a, L_{as}$ を計算します。計算方法には、最大値、最小値や平均値から簡易的に求める方法や、より厳密な手法として、最小二乗法等の統計的手法を用いる場合もあります。
また $L_{lcr}$ と $L_d, L_q$ には以下の関係があります。
$$ L_{lcr} = \left( L_d + L_q \right) – \left( L_d – L_q \right) \cos \left( 2 \theta – \frac{2 \pi }{3} \right) $$
したがって、d,q 軸インダクタンスは $L_{lcr}$ の最大/最小値から求められます。
$$
\begin{matrix}
L_d = \frac{1}{2} \min_{\theta} \{ L_{lcr} \}\\
L_q = \frac{1}{2} \max_{\theta} \{ L_{lcr} \}\\
\end{matrix}
$$
回転子位置に対するインダクタンスの測定結果が高調波の影響により歪んでいる場合、単に最大・最小値を取るよりも基本波の振幅を計算する方が正確です。
2.2 中性点が引き出せない場合2
※本節の手法は間違いの可能性があります、現在検証中です(230116)
⇒間違っていませんでした。文献を追加しました。(230122)
v-w相間を短絡させて測定する手法もあります。
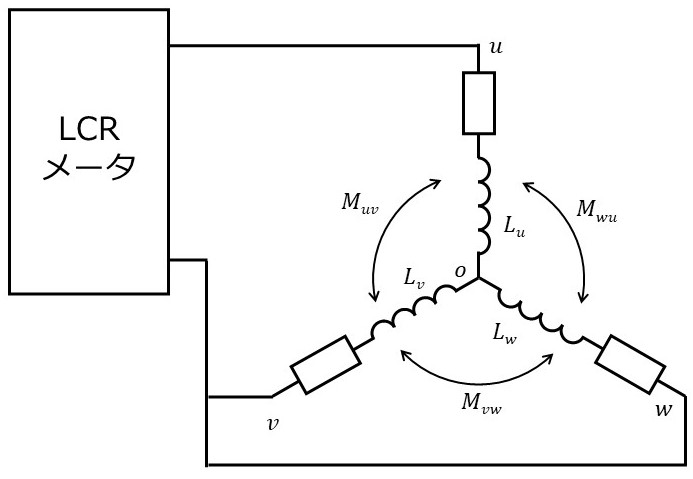
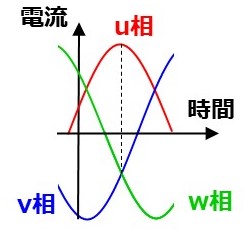
この場合、v, w相のインピーダンスが同じと仮定すると、電流状態は $i_u = I, i_v = i_w = -I/2$ となり、これは3相平衡電流の一状態です。(図の破線の状態;交流電流が流れるので厳密には異なる。)ちょうどステータ巻線の成す磁束ベクトルが u相方向を向いている状態ですね。
3相の電圧方程式のインダクタンスに関する項は、次式のようになります。
$$
\begin{pmatrix}
v_u \\
v_v \\
v_w \\
\end{pmatrix} = \cdots + \frac{d}{dt} \\
\begin{pmatrix}
L_u & M_{uv} & M_{wu} \\
M_{uv} & L_v & M_{vw} \\
M_{wu} & M_{vw} & L_w \\
\end{pmatrix} \\
\begin{pmatrix}
1 \\
-\frac{1}{2} \\
-\frac{1}{2} \\
\end{pmatrix} I + \cdots
$$
したがって、u-v相間の電圧方程式から、LCRメータで計測できるインダクタンス成分 $L_{lcr}$ は次のように求まります。
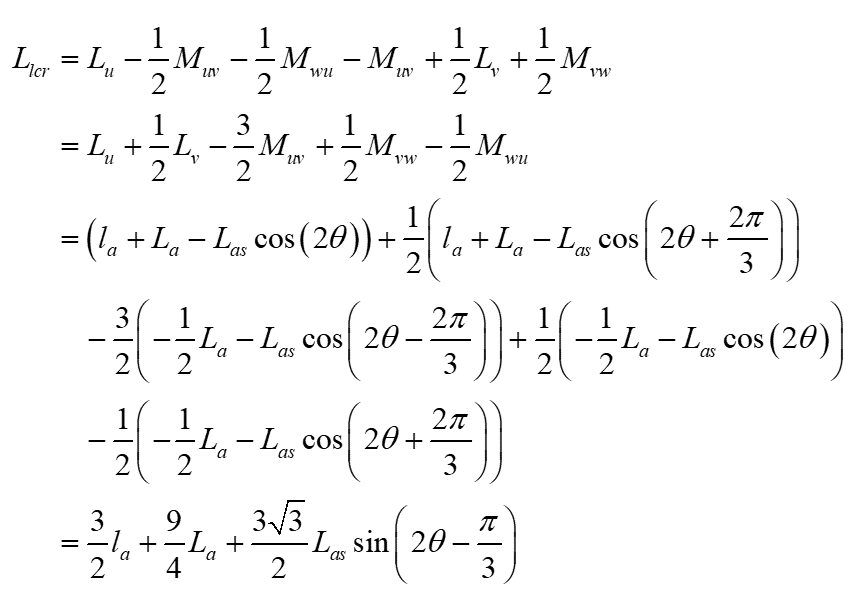
2.1節と同様に、回転子位置を変えながらインダクタンスを測定することで、各パラメータが計算できます。
このインダクタンスは、回転子が $ \theta = 0^\circ$(d 軸が α 軸と一致)と $ \theta = 90^\circ$(d 軸が β 軸と一致)に固定されているとき、d,q 軸インダクタンスとの関係性がクリアになります。
$$
\begin{matrix}
L_{lcr} (\theta = 0^\circ) = \frac{3}{2} L_d \\
L_{lcr} (\theta = 90^\circ) = \frac{3}{2} L_q \\
\end{matrix}
$$
2.1 節に比べた本手法の利点は、モータ内部の磁化状態がより実運転状態に近づくという点です。コアの磁気飽和の度合いは測定されるインダクタンスに非常に大きな影響を及ぼします。最初に述べた通り、v,w 相間を短絡した状態で直流電圧を印加すると、回転磁界の一つの状態を模擬することとなり、実駆動に近い状態での測定ができます。ただし、本記事の設定では LCR メータにより交流電流を通電するため、特に d 軸の減磁/着磁方向における磁束の反転が生じるという点で、厳密には実駆動状態とは異なります。文献 [1] では、q 軸方向は正負の励磁が同パターンなので交流でも問題なく、$i_d = 0$ 制御の駆動状態と同じインダクタンスが測定できる、と述べられています。
文献 [1] では、2.1, 2.2 節の接続状態で直流電圧を印加した場合のインダクタンス測定方法に関しても説明していますが、本記事は LCR メータで気軽にインダクタンスを測定しようという趣旨なので割愛します。
2.3 中性点が引き出せる場合
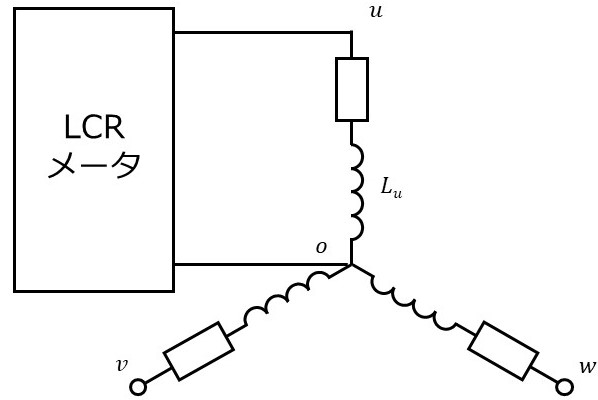
(これは完全に主観ですが)相互インダクタンスの取り扱いは難しく、1章のモデリングの正しさは必ずしも保証できません。そこで、中性点が引き出せる場合は、u相-中性点間にLCRメータを接続することで、相互インダクタンスの影響を無視した計測が行えます。この場合、LCRメータで計測できるインダクタンス成分は次式の通りです。
$$ L_{lcr} = L_u = l_a + L_a – L_{as} \cos \left( 2 \theta \right) $$
2.1節と同様に、回転子位置を変えながらインダクタンスを測定することで、各パラメータが計算できます。
3. 補足
本記事の計測手法はあくまで簡易的なものです。目的にも寄りますが、例えば制御に使用するパラメータが欲しい場合には、電圧と電流から計算したほうが厳密です。特に大容量のモータでは、局所的な磁気飽和によってインダクタンスが大きく変化するので、通電状態でインダクタンスを計測すべきです。
4. 参考文献
以上です。質問・コメント等ございましたら、メールやTwitterよりご連絡ください。