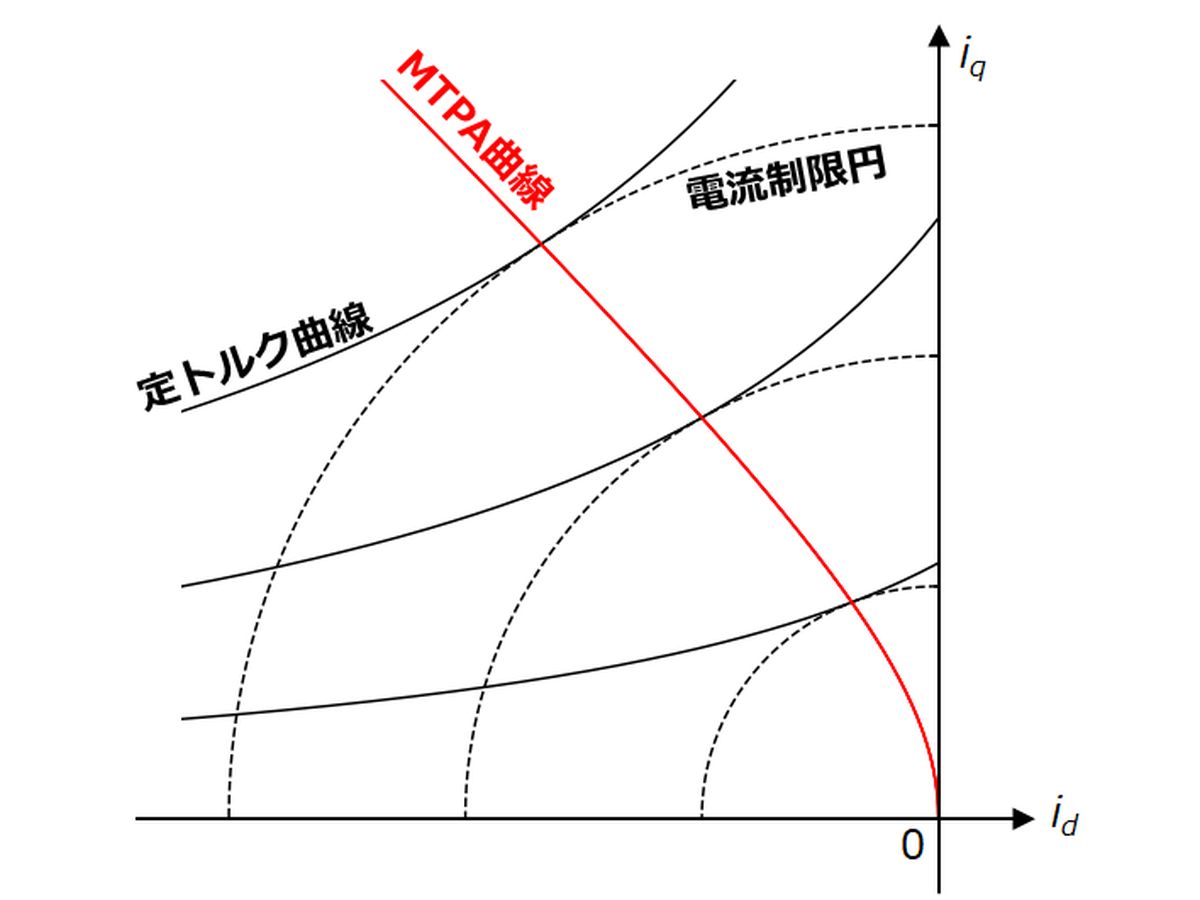
埋込磁石同期モータ(IPMSM: Interior Permanent Magnet Synchronous Motor)の代表的な制御法として,最大トルク/電流(MTPA: Maximum Torque Per Ampere)制御があります。
モータパラメータが一定の場合,MTPA制御時の電流ベクトルの関係は,電機子電流 $I_a$, 電流位相 $\beta$ とすると,以下のように表すことができます。
$$ \sin \beta=\frac{-\varPsi_a+\sqrt{\varPsi_{a}^{2}+8 \left( L_q – L_d \right)^2 I_a^2}}{4 \left( L_q – L_d \right) I_a} $$
ここで,$\varPsi_a$は永久磁石による電機子鎖交磁束,$L_d , L_q$はd, q軸インダクタンスです。
この式の導出は簡単です。↓で解説しています。
また,MTPA制御曲線をd,q軸電流 $i_d , i_q$ で表すと,次式のようになります。
$$ i_d=\frac{\varPsi_a}{2 \left( L_q – L_d \right)}-\sqrt{\frac{\varPsi_a^2}{4 \left( L_q – L_d \right)^2} + i_q^2} $$
本記事では,こちらのid-iq平面上におけるMTPA制御曲線の関係式を導出します。
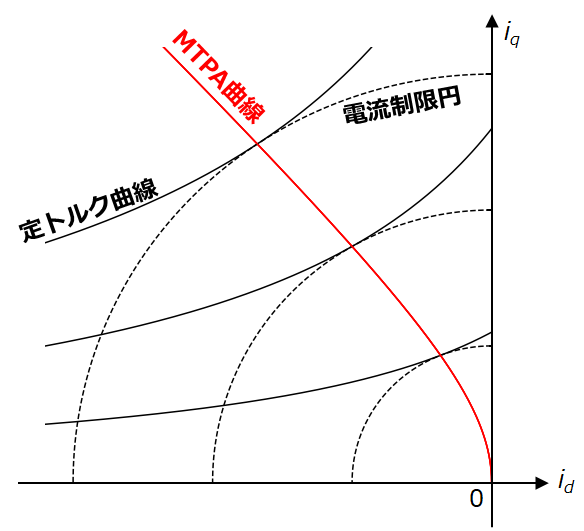
本記事は対象を $L_d < L_q$ のIPMSM(逆突極機など)に絞りますが,$L_d > L_q$ の巻線界磁形同期モータや同期リラクタンスモータでも同様の議論が行えます。(定義を少し変える必要があります。)
1. 問題の定義
まず,絶対変換を仮定して,トルク式を次式で定義します。
$$ T=P_n \left( \varPsi_a i_q + \left( L_d – L_q \right) i_d i_q \right) $$
$$ T=P_n \left( \varPsi_a I_a \cos \beta + \frac{1}{2} \left( L_q – L_d \right) I_a^2 \sin{2 \beta} \right) $$
ここで,$P_n$ は極対数です。コギングトルクなどの平均0の項は無視しています。
$I_a , \beta$ による表現では,$I_a$ を一定値 $I_a^*$ として $\beta$ に対するトルクの最大化を考えました。
$$ \max_{\beta} T \quad s.t. \quad I_{a} = I_{a}^{*} $$
これは,トルクを一定値 $T^*$ とした場合の $I_a$ の最小化問題と等価です。そのため,以下の最小化問題を考えます。
$$ \min_{i_d , i_q} I_a = \sqrt{i_d^2+i_q^2} \quad s.t. \quad T = T^{*} $$
2. MTPA曲線の導出
定義した $I_a$ の最小化問題は凸最適化問題なので,ラグランジュ乗数 $\lambda \in \mathbb{R}$ を導入して,以下のラグランジュ関数(ラグラジアン)を考えます。
$$ L\left( i_d , i_q , \lambda \right) = \sqrt{i_d^2+i_q^2} + \lambda \left( T – T^{*} \right) $$
ラグランジュの未定乗数法より,以下の関係式が得られます。ここで, $i_d^2+i_q^2 > 0$ と仮定しました。($i_d=i_q=0$ も解候補であることは明らかです。)
$$ \frac{\partial}{\partial \lambda} L\left( i_d , i_q , \lambda \right) = T – T^{*} = 0 $$
$$ \frac{\partial}{\partial i_d} L\left( i_d , i_q , \lambda \right) = \frac{i_d}{\sqrt{i_d^2+i_q^2}} + \lambda \frac{\partial}{\partial i_d} T=0 $$
$$ \frac{\partial}{\partial i_q} L\left( i_d , i_q , \lambda \right) = \frac{i_q}{\sqrt{i_d^2+i_q^2}} + \lambda \frac{\partial}{\partial i_q} T=0 $$
第2,3式からラグランジュ乗数を消去すると,次式が得られます。
$$ i_q \frac{\partial}{\partial i_d} T = i_d \frac{\partial}{\partial i_q} T $$
トルクのid, iqによる微分はそれぞれ
$$ \frac{\partial}{\partial i_d} T = P_n \left( L_d – L_q \right) i_q $$
$$ \frac{\partial}{\partial i_q} T = P_n\left( \varPsi_a + \left( L_d – L_q \right) i_d \right) $$
となるので,これらを先の関係式に代入すると,
$$ i_q P_n \left( L_d – L_q \right) i_q = i_d P_n\left( \varPsi_a + \left( L_d – L_q \right) i_d \right) $$
$$ \left( L_d – L_q \right) i_d^2 + \varPsi_a i_d – \left( L_d – L_q \right) i_q^2 = 0 $$
という関係式が得られます。これは,id-iq平面上の双曲線を表しています。
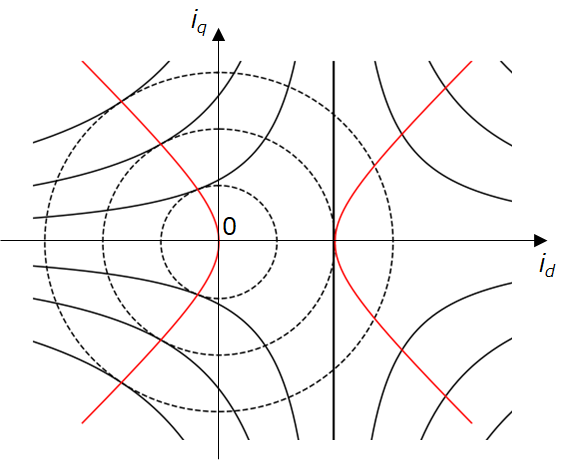
よって,2次方程式の解の公式と $i_d<0$ の条件から,id-iq平面上のMTPA曲線の一般式が得られます。
$$ i_d=\frac{\varPsi_a}{2 \left( L_q – L_d \right)} – \sqrt{\frac{\varPsi_a^2}{4 \left( L_q – L_d \right)^2} + i_q^2} $$
(この式は厳密には解候補ですが,十分性の証明は省略します。)
以上です。質問・コメント等ございましたら、メールやTwitterよりご連絡ください。
3. 参考文献
- 森本茂雄,真田雅之,省エネモータの原理と設計法,科学情報出版株式会社 (2013)
- 新中新二,永久磁石同期モータのベクトル制御技術 上巻,電波新聞社 (2008)
- Anton Dianov et al., IEEE Trans. Power Electron., vol. 37, no. 4, pp. 3990-4007, 2022