ライブラリのバージョンアップ(0.6.0)で使用方法がガラッと変わってしまったので、近々修正予定です(22/12/03)⇒修正完了しました(22/12/17)
pymoo は多目的最適化に特化した Python ライブラリです。
最適化分野で有名な Kalyanmoy Deb 教授の研究室の Julian Blank らが開発しました。
公式ドキュメント GitHub 論文
日本語解説記事がほとんど見当たらないので,自分用にまとめます。
何はともあれインストール。
$ pip install -U pymoo==0.6.0
- 0. プログラム例
- 1. 問題の設定
- 2. アルゴリズムの選択
- 2.1 遺伝的アルゴリズム(GA: Genetic Algorithm)
- 2.2 差分進化法(DE: Differential Evolution)
- 2.3 粒子群最適化(PSO: Particle Swarm Optimization)
- 2.4 NSGA-II (Non-dominated Sorting Genetic Algorithm)
- 2.5 R-NSGA-II
- 2.6 NSGA-III
- 2.7 U-NSGA-III
- 2.8 R-NSGA-III
- 2.9 BRKGA (Biased Random Key Genetic Algorithm)
- 2.10 Nelder-Mead法
- 2.11 Hooke-Jeevesパターン探索法
- 2.12 CMA-ES (Covariance Matrix Adaptation Evolution Strategy)
- 2.13 MOEA/D (Multiobjective Evolutionary Algorithm based on Decomposition)
- 2.14 C-TAEA
- 3. 終了条件の定義
- 4. 最適化の実行
- 5. 結果の検討
0. プログラム例
多目的最適化プログラム例を掲載します。
とりあえず使ってみたいんじゃあ,って人はこちらからどうぞ。
import numpy as np
from pymoo.util.misc import stack
from pymoo.core.problem import Problem
from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.operators.sampling.lhs import LHS
from pymoo.operators.crossover.sbx import SBX
from pymoo.operators.mutation.pm import PolynomialMutation
from pymoo.termination import get_termination
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter
# 問題設定(自作関数)
class MyProblem(Problem):
def __init__(self):
super().__init__(n_var=2,
n_obj=2,
n_constr=2,
xl=np.array([-2,-2]),
xu=np.array([2,2]),
)
def _evaluate(self, X, out, *args, **kwargs):
f1 = X[:,0]**2 + X[:,1]**2
f2 = (X[:,0]-1)**2 + X[:,1]**2
g1 = 2*(X[:, 0]-0.1) * (X[:, 0]-0.9) / 0.18
g2 = - 20*(X[:, 0]-0.4) * (X[:, 0]-0.6) / 4.8
out["F"] = np.column_stack([f1, f2])
out["G"] = np.column_stack([g1, g2])
# パレート解の設定
# パレート解が既知の場合に使用(テスト用)
def func_pf(flatten=True, **kwargs):
f1_a = np.linspace(0.1**2, 0.4**2, 100)
f2_a = (np.sqrt(f1_a) - 1)**2
f1_b = np.linspace(0.6**2, 0.9**2, 100)
f2_b = (np.sqrt(f1_b) - 1)**2
a, b = np.column_stack([f1_a, f2_a]), np.column_stack([f1_b, f2_b])
return stack(a, b, flatten=flatten)
def func_ps(flatten=True, **kwargs):
x1_a = np.linspace(0.1, 0.4, 50)
x1_b = np.linspace(0.6, 0.9, 50)
x2 = np.zeros(50)
a, b = np.column_stack([x1_a, x2]), np.column_stack([x1_b, x2])
return stack(a,b, flatten=flatten)
class MyTestProblem(MyProblem):
def _calc_pareto_front(self, *args, **kwargs):
return func_pf(**kwargs)
def _calc_pareto_set(self, *args, **kwargs):
return func_ps(**kwargs)
if __name__ == "__main__":
# 問題の定義
problem = MyTestProblem()
# アルゴリズムの初期化(NSGA-IIを使用)
algorithm = NSGA2(
pop_size=40,
n_offsprings=10,
sampling=LHS(),
crossover=SBX(prob=0.9, eta=15),
mutation=PolynomialMutation(eta=20),
eliminate_duplicates=True
)
# 終了条件(40世代)
termination = get_termination("n_gen", 40)
# 最適化の実行
res = minimize(problem,
algorithm,
termination,
seed=1,
save_history=True,
verbose=True)
# 結果の可視化
ps = problem.pareto_set(use_cache=False, flatten=False)
pf = problem.pareto_front(use_cache=False, flatten=False)
# 入力変数空間
# plot = Scatter(title = "Design Space", axis_labels="x")
# plot.add(res.X, s=30, facecolors='none', edgecolors='r')
# if ps is not None:
# plot.add(ps, plot_type="line", color="black", alpha=0.7)
# plot.do()
# plot.apply(lambda ax: ax.set_xlim(-0.5, 1.5))
# plot.apply(lambda ax: ax.set_ylim(-2, 2))
# plot.show()
# 目的関数空間
plot = Scatter(title = "Objective Space")
plot.add(res.F)
if pf is not None:
plot.add(pf, plot_type="line", color="black", alpha=0.7)
plot.show()
1. 問題の設定
1.1 自作関数
1.1.1 設定する問題の詳細
下記の問題を自作する場合を考えます。
$$\begin{eqnarray}\min\quad f_{1}\left(x\right)&=&\left(x^{2}_{1}+x^{2}_{2}\right) \\
\max\quad f_{2}\left(x\right)&=&-\left(x_{1}-1\right)^{2}-x^{2}_{2} \\
\textup{s.t.}\quad g_{1}\left(x\right)&=&2\left(x_{1}-0.1\right)\left(x_{1}-0.9\right)\leq 0 \\
g_{2}\left(x\right)&=&20\left(x_{1}-0.4\right)\left(x_{1}-0.6\right)\geq 0 \\
\qquad -2&\leq& x_{1}\leq2\\
\qquad 2&\leq& x_{2}\leq2 \end{eqnarray}$$
pymooでは最小化問題を設定するため,最大化問題は-1をかけて最小化問題に変換します。
制約条件は $\leq0$ 制約を設定するため,こちらも-1をかけて変換します。
全て制約条件を同等に扱うため,制約条件を正規化することが推奨されています。
$$\begin{eqnarray}\min\quad f_{1}\left(x\right)&=&\left(x^{2}_{1}+x^{2}_{2}\right) \\
\min\quad f_{2}\left(x\right)&=&\left(x_{1}-1\right)^{2}+x^{2}_{2} \\
\textup{s.t.}\quad g_{1}\left(x\right)&=&2\left(x_{1}-0.1\right)\left(x_{1}-0.9\right) / 0.18\leq 0 \\
g_{2}\left(x\right)&=&-20\left(x_{1}-0.4\right)\left(x_{1}-0.6\right)/4.8\leq 0 \\
\qquad -2&\leq& x_{1}\leq2\\
\qquad 2&\leq& x_{2}\leq2 \end{eqnarray}$$
ここで,正規化の係数はそれぞれ $2*(-0.1)*(-0.9)=0.18$,$20*(-0.4)*(-0.6)=4.8$ から算出しています。
1.1.2 Classによる設定
Classによる問題設定は,集団内の全ての個体を一括処理する Vectorized Evaluation と,1個体ずつ処理する Elementwise Evaluation があります。
Vectorized Evaluation
評価関数に入力される変数Xは,全ての個体が格納された2次元のndarray形式です。
1軸目が各個体を表すため,2軸目の値を計算に用います。
import numpy as np
from pymoo.core.problem import Problem
class MyProblem(Problem):
def __init__(self):
super().__init__(n_var=2, # 入力変数の次元
n_obj=2, # 目的関数の数
n_constr=2, # 制約条件の数
xl=np.array([-2,-2]), # 入力変数の下限
xu=np.array([2,2]), # 入力変数の上限
)
def _evaluate(self, X, out, *args, **kwargs):
# 目的関数
f1 = X[:,0]**2 + X[:,1]**2
f2 = (X[:,0]-1)**2 + X[:,1]**2
# 制約条件
g1 = 2*(X[:, 0]-0.1) * (X[:, 0]-0.9) / 0.18
g2 = - 20*(X[:, 0]-0.4) * (X[:, 0]-0.6) / 4.8
out["F"] = np.column_stack([f1, f2])
out["G"] = np.column_stack([g1, g2])
problem = MyProblem()| 主な引数 | 説明 |
| n_var | 入力変数の数(整数) |
| n_obj | 目的関数の数(整数) |
| n_constr | 制約条件の数(整数) |
| xl | 入力変数の下限値(整数/np.ndarray,長さn_var) |
| xu | 入力変数の上限値(整数/np.ndarray,長さn_var) |
関数の評価は_evaluateメソッドで行われ,out["F"]に評価関数の値,out["G"]に制約条件の値を書き込みます。
Elementwise Evaluation
Elementwise形式では各個体を一つずつ処理します。
Elementwise形式を使用する場合は,elementwise_evaluation=Trueと設定する必要があります。
一括処理できる場合はVectorize形式のほうが早いため,一括処理ができない場合に使用します。
import numpy as np
from pymoo.core.problem import ElementwiseProblem
class MyProblem(ElementwiseProblem):
def __init__(self):
super().__init__(n_var=2, # 入力変数の次元
n_obj=2, # 目的関数の数
n_constr=2, # 制約条件の数
xl=np.array([-2,-2]), # 入力変数の下限
xu=np.array([2,2]), # 入力変数の上限
)
def _evaluate(self, x, out, *args, **kwargs):
# 目的関数
f1 = x[0]**2 + x[1]**2
f2 = (x[0]-1)**2 + x[1]**2
# 制約条件
g1 = 2*(x[0]-0.1) * (x[0]-0.9) / 0.18
g2 = - 20*(x[0]-0.4) * (x[0]-0.6) / 4.8
out["F"] = [f1, f2]
out["G"] = [g1, g2]
problem = MyProblem()1.1.3 関数による設定
pymooでは関数による定義にも対応しています。
定義を簡略化できますが,シンプルな関数を定義する場合にのみ使用することが推奨されています。
import numpy as np
from pymoo.problems.functional import FunctionalProblem
# 目的関数
objs = [
lambda x: x[0]**2 + x[1]**2,
lambda x: (x[0]-1)**2 + x[1]**2
]
# 制約条件
constr_ieq = [
lambda x: 2*(x[0]-0.1) * (x[0]-0.9) / 0.18,
lambda x: - 20*(x[0]-0.4) * (x[0]-0.6) / 4.8
]
functional_problem = FunctionalProblem(2,
objs,
constr_ieq=constr_ieq,
xl=np.array([-2,-2]),
xu=np.array([2,2]))| 主な引数 | 説明 |
| n_var | 入力変数の数 (int) |
| objs | 目的関数 |
| constr_ieq | 制約条件(不等式制約) |
| constr_eq | 制約条件(等式制約) |
| constr_eq_eps | 等式制約の許容誤差 |
| xl | 入力変数の下限値 (float) |
| xu | 入力変数の上限値 (float) |
| func_pf | パレートフロント(後述) |
| func_ps | パレートセット(後述) |
1.1.4 (任意指定)パレートフロントとパレートセット
問題の最適解が既知の場合には,パレートフロントとパレートセットを設定することでアルゴリズムの収束を判定できます。
関数の最適化のみを目的とする場合には,この設定は必要ありません。
- 共通設定
from pymoo.util.misc import stack
def func_pf(flatten=True, **kwargs):
f1_a = np.linspace(0.1**2, 0.4**2, 100)
f2_a = (np.sqrt(f1_a) - 1)**2
f1_b = np.linspace(0.6**2, 0.9**2, 100)
f2_b = (np.sqrt(f1_b) - 1)**2
a, b = np.column_stack([f1_a, f2_a]), np.column_stack([f1_b, f2_b])
return stack(a, b, flatten=flatten)
def func_ps(flatten=True, **kwargs):
x1_a = np.linspace(0.1, 0.4, 50)
x1_b = np.linspace(0.6, 0.9, 50)
x2 = np.zeros(50)
a, b = np.column_stack([x1_a, x2]), np.column_stack([x1_b, x2])
return stack(a,b, flatten=flatten)- Classによる設定の場合
import numpy as np
from pymoo.util.misc import stack
from pymoo.core.problem import Problem
class MyTestProblem(MyProblem):
def __init__(self):
'''省略'''
def _evaluate(self, X, out, *args, **kwargs):
'''省略'''
def _calc_pareto_front(self, *args, **kwargs):
return func_pf(**kwargs)
def _calc_pareto_set(self, *args, **kwargs):
return func_ps(**kwargs)
problem = MyTestProblem()- 関数による設定の場合
from pymoo.problems.functional import FunctionalProblem
functional_test_problem = FunctionalProblem(2,
objs,
constr_ieq=constr_ieq,
xl=-2,
xu=2,
func_pf=func_pf,
func_ps=func_ps
)1.1.5 並列化
解評価の並列化により,最適化計算を高速化することができます。最も簡単な方法は,Vectorized 形式により Numpy 行列を利用することであり,これが公式にも推奨されています。
Elementwise 形式で利用できる並列化手法として,Python の標準ライブラリ multiprocessing.Pool.starmap で定義される starmap オブジェクトを利用可能です。
次の問題を考えます。
from pymoo.core.problem import ElementwiseProblem
class MyProblem(ElementwiseProblem):
def __init__(self, **kwargs):
super().__init__(n_var=10, n_obj=1, n_constr=0, xl=-5, xu=5, **kwargs)
def _evaluate(self, x, out, *args, **kwargs):
out["F"] = (x ** 2).sum()スレッド数を指定したり,
from multiprocessing.pool import ThreadPool
from pymoo.algorithms.soo.nonconvex.ga import GA
from pymoo.optimize import minimize
n_threads = 8 # スレッド数
pool = ThreadPool(n_threads) # 初期化
problem = MyProblem(parallelization = ('starmap', pool.starmap)) # 問題設定
res = minimize(problem, GA()) # 計算の実行
print(f'Threads: {res.exec_time} sec')
pool.close()Threads: 0.8782460689544678 sec
プロセス数を指定することが可能です。
import multiprocessing
from pymoo.algorithms.soo.nonconvex.ga import GA
from pymoo.optimize import minimize
n_process = 8 # プロセス数
pool = multiprocessing.Pool(n_process) # 初期化
problem = MyProblem(parallelization = ('starmap', pool.starmap)) # 問題設定
res = minimize(problem, GA()) # 計算の実行
print(f'Processes: {res.exec_time} sec')
pool.close()Processes: 11.800267219543457 sec
また,ライブラリ Dask による分散処理にも対応しています。
from dask.distributed import Client
import numpy as np
from pymoo.core.problem import ElementwiseProblem
from pymoo.algorithms.soo.nonconvex.ga import GA
from pymoo.optimize import minimize
client = Client()
# 評価関数の定義
def fun(x):
return {
"F": np.sum(x ** 2)
}
# 問題の定義(評価関数は使用しない)
class MyProblem(ElementwiseProblem):
def __init__(self, *args, **kwargs):
super().__init__(n_var=10, n_obj=1, n_constr=0, xl=-5, xu=5, *args, **kwargs)
# 問題を作成し,並列化をdaskに設定
problem = MyProblem(parallelization=("dask", client, fun))
# 実行
res = minimize(problem, GA())
print(f'Dask: {res.exec_time} sec')
client.close()Dask: 54.45502281188965 sec
並列化のプロセスをよりカスタマイズしたい場合には,問題の定義の際に並列化を組み込みます。問題定義のデフォルト設定はVectorized 形式であることに注意する必要があります
スレッド数の例は以下の通り,
from multiprocessing.pool import ThreadPool
from pymoo.core.problem import Problem
import numpy as np
from pymoo.algorithms.soo.nonconvex.ga import GA
from pymoo.optimize import minimize
class MyProblem(Problem):
def __init__(self, **kwargs):
super().__init__(n_var=10, n_obj=1, n_constr=0, xl=-5, xu=5, **kwargs)
self.pool = ThreadPool(8)
def _evaluate(self, X, out, *args, **kwargs):
# 評価関数の定義
def my_eval(x):
return (x ** 2).sum()
# 変数の処理
params = [[X[k]] for k in range(len(X))]
# 関数値を並列処理で計算
F = self.pool.starmap(my_eval, params)
# 関数値を返す
out["F"] = np.array(F)
problem = MyProblem()
res = minimize(MyProblem(), GA())
print(f'Threads: {res.exec_time} sec')
problem.pool.close()Threads: 1.0203194618225098 sec
Dask を使用した例は以下の通りです。
import numpy as np
from dask.distributed import Client
from pymoo.algorithms.soo.nonconvex.ga import GA
from pymoo.core.problem import Problem
from pymoo.optimize import minimize
class MyProblem(Problem):
def __init__(self, client, *args, **kwargs):
super().__init__(n_var=10, n_obj=1, n_constr=0, xl=-5, xu=5, *args, **kwargs)
self.client = client
def _evaluate(self, X, out, *args, **kwargs):
def fun(x):
return np.sum(x ** 2)
jobs = [self.client.submit(fun, x) for x in X]
out["F"] = np.row_stack([job.result() for job in jobs])
client = Client(processes=False)
problem = MyProblem(client)
res = minimize(problem, GA())
print(f'Dask: {res.exec_time} sec')
client.close()Dask: 26.734183311462402 sec
1.2 制約条件の取り扱い
1.2.1 不等式制約
以下の不等式制約付き最適化問題を考えます。
$$\begin{eqnarray} \min&\quad& f\left(x\right)=x^2_1+x^2_2 \\
\textup{s.t.}&\quad& x_1 + x_2 \geq 1 \\
&\quad&0\leq x\leq 2 \\
&\quad&0\leq x\leq 2\end{eqnarray}$$
pymooでは不等式制約を扱うため,この制約を以下のように不等式の形式で表現します。
$$ 1-(x_1 + x_2)\leq 0 $$
これまでの議論から,制約条件を実装すると,下記のようになります。
from pymoo.core.problem import ElementwiseProblem
import numpy as np
import matplotlib.pyplot as plt
class ConstrainedProblem(ElementwiseProblem):
def __init__(self, **kwargs):
super().__init__(n_var=2, n_obj=1, n_ieq_constr=1, n_eq_constr=0, xl=0, xu=2, **kwargs)
def _evaluate(self, x, out, *args, **kwargs):
out["F"] = x[0] ** 2 + x[1] ** 2
out["G"] = 1.0 - (x[0] + x[1])
X1, X2 = np.meshgrid(np.linspace(0, 2, 500), np.linspace(0, 2, 500))
F = X1**2 + X2**2
plt.rc('font', family='serif')
levels = 5 * np.linspace(0, 1, 10)
plt.figure(figsize=(7, 5))
CS = plt.contour(X1, X2, F, levels, colors='black', alpha=0.5)
CS.collections[0].set_label("$f(x)$")
X = np.linspace(0, 1, 500)
plt.plot(X, 1-X, linewidth=2.0, color="green", linestyle='dotted', label="g(x)")
plt.scatter([0.5], [0.5], marker="*", color="red", s=200, label="Optimum (0.5, 0.5)")
plt.xlim(0, 2)
plt.ylim(0, 2)
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.legend(loc='upper center', bbox_to_anchor=(0.5, 1.12),
ncol=4, fancybox=True, shadow=False)
plt.tight_layout()
plt.show()
1.2.2 等式制約
以下の等式制約付き最適化問題を考えます。
$$\begin{eqnarray} \min&\quad& f\left(x\right)=x^2_1+x^2_2 \\
\textup{s.t.}&\quad& x_1 + x_2 \geq 1 \\
&\quad&3 x_1 – x_2 = 0 \\
&\quad&0\leq x\leq 2 \\
&\quad&0\leq x\leq 2\end{eqnarray}$$
制約条件を実装すると,下記のようになります。
import numpy as np
import matplotlib.pyplot as plt
from pymoo.core.problem import ElementwiseProblem
class ConstrainedProblemWithEquality(ElementwiseProblem):
def __init__(self, **kwargs):
super().__init__(n_var=2, n_obj=1, n_ieq_constr=1, n_eq_constr=1, xl=0, xu=1, **kwargs)
def _evaluate(self, x, out, *args, **kwargs):
out["F"] = x[0] + x[1]
out["G"] = 1.0 - (x[0] + x[1])
out["H"] = 3 * x[0] - x[1]
X1, X2 = np.meshgrid(np.linspace(0, 2, 500), np.linspace(0, 2, 500))
F = X1**2 + X2**2
plt.rc('font', family='serif')
levels = 5 * np.linspace(0, 1, 10)
plt.figure(figsize=(7, 5))
CS = plt.contour(X1, X2, F, levels, colors='black', alpha=0.5)
CS.collections[0].set_label("$f(x)$")
X = np.linspace(0, 1, 500)
plt.plot(X, 1-X, linewidth=2.0, color="green", linestyle='dotted', label="g(x)")
plt.plot(X, 3*X, linewidth=2.0, color="blue", linestyle='dotted', label="h(x)")
plt.scatter([0.25], [0.75], marker="*", color="red", s=200, label="Optimum (0.5, 0.5)")
plt.xlim(0, 2)
plt.ylim(0, 2)
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.legend(loc='upper center', bbox_to_anchor=(0.5, 1.12),
ncol=4, fancybox=True, shadow=False)
plt.tight_layout()
plt.show()
1.2.3 パラメータレス制約処理(Feasbility First)
パラメータレス制約処理は pymoo のデフォルトの制約処理方法です。実現不可能解よりも実現可能な解を厳密に優先します。
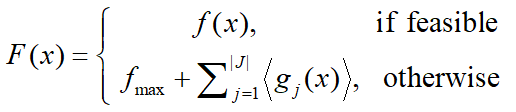
ここで,⟨⋅⟩ は次のように定義します。
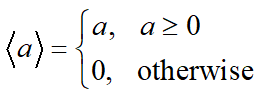
この方法は,アルゴリズムが比較に基づいて各個体を取捨選択する際に有効です。例えば,遺伝的アルゴリズムでは,どの個体が生存するか選択する際に,この方法を用いることで実行可能解が優先的に選択されます。
1.2.4 ペナルティ法
全てを紹介しているわけではないので、詳細はこちらを参照してください。
ペナルティ法では,全ての不等式制約を目的値にペナルティ関数として与えます。制約条件は不等式制約に変換して計算します。
$$F\left(x\right)=f\left(x\right)+\mu P\left(x\right)$$
ここで,$\mu>0$ は定数,ペナルティ関数 $P\left(x\right)$ は次式で定義します。
$$P\left(x\right)=\sum^{|J|}_{j=1}{\langle g_{j}\left(x\right) \rangle}$$
from pymoo.algorithms.soo.nonconvex.de import DE
from pymoo.constraints.as_penalty import ConstraintsAsPenalty
from pymoo.optimize import minimize
from pymoo.core.evaluator import Evaluator
from pymoo.core.individual import Individual
problem = ConstrainedProblem()
algorithm = DE()
res = minimize(ConstraintsAsPenalty(problem, penalty=100.0),
algorithm,
seed=1,
verbose=False)
res = Evaluator().eval(problem, Individual(X=res.X))
print("Best solution found: \nX = %s\nF = %s\nCV = %s" % (res.X, res.F, res.CV))1.2.5 修正オペレータ
単純なアプローチとして,制約を違反する解を制約内に修正する修正オペレータも使用可能です。これは,制約の方程式が明らかな場合にのみ可能です。
Repair クラスを定義します。Repair クラスでは,各個体を実現可能解とするために,$x_0=x_1 /3$ と修正するよう実装します。
from pymoo.core.repair import Repair
class MyRepair(Repair):
def _do(self, problem, X, **kwargs):
X[:, 0] = 1/3 * X[:, 1]
return X修正オペレータを用いた最適化は以下のように初期化,実行します。
from pymoo.algorithms.soo.nonconvex.ga import GA
from pymoo.optimize import minimize
algorithm = GA(repair=MyRepair())
res = minimize(ConstrainedProblemWithEquality(),
algorithm,
('n_gen', 20),
seed=1,
verbose=True)
print("Best solution found: \nX = %s\nF = %s\nCV = %s" % (res.X, res.F, res.CV))
1.3 ベンチマーク関数
pymooでは有名なベンチマーク関数が数多く実装されており,get_problem関数から使用することができます。
from pymoo.problems import get_problem
problem = get_problem("zdt1") # zdt1の場合
使用可能なベンチマーク関数一覧は 公式ドキュメント を参照ください。
2. アルゴリズムの選択
続いて,最適化アルゴリズムの選択を行います。
2.1 遺伝的アルゴリズム(GA: Genetic Algorithm)
皆さんご存じ遺伝的アルゴリズム。単目的最適化用に実装されているようです。
from pymoo.algorithms.soo.nonconvex.ga import GA
from pymoo.factory import get_problem
from pymoo.optimize import minimize
problem = get_problem("g1")
algorithm = GA(
pop_size=100,
eliminate_duplicates=True)
res = minimize(problem,
algorithm,
seed=1,
verbose=False)
print("Best solution found: \nX = %s\nF = %s" % (res.X, res.F))| 主な引数 | 説明 |
| pop_size | 集団サイズ (int) |
| sampling | 初期集団のサンプリング方法(2.2.1項参照) |
| selection | 選択(2.2.2項参照) |
| crossover | 交叉(2.2.3項参照) |
| mutation | 突然変異(2.2.4項参照) |
| eliminate_duplicates | 親と子の集団内での重複を排除するか (bool) |
| n_offsprings | 交配によって作られる子孫の数 (int) デフォルトは集団サイズ |
2.2.1 Sampling
初期集団のサンプリング方法は、ランダムサンプリングとラテン超方格法(LHS)の2種類が用意されています。
from pymoo.core.problem import Problem
from pymoo.operators.sampling.rnd import FloatRandomSampling
from pymoo.util import plotting
problem = Problem(n_var=2, xl=0, xu=1)
sampling = FloatRandomSampling()
X = sampling(problem, 200).get("X")
plotting.plot(X, no_fill=True)from pymoo.operators.sampling.lhs import LHS
sampling = LHS()
X = sampling(problem, 200).get("X")
plotting.plot(X, no_fill=True)2.2.2 Selection
Selection モジュールでは以下の2種類の選択方法を指定可能です。
| random | ランダム選択 |
| tournament | トーナメント選択 |
from pymoo.algorithms.soo.nonconvex.ga import GA
from pymoo.operators.selection.rnd import RandomSelection
selection = RandomSelection()
algorithm = GA(
pop_size=100,
selection=selection,
eliminate_duplicates=True)トーナメント選択では,比較に必要な関数の情報も必要です。以下はバイナリトーナメント方式の例です。
from pymoo.algorithms.soo.nonconvex.ga import GA
from pymoo.operators.selection.tournament import TournamentSelection
from pymoo.optimize import minimize
from pymoo.problems import get_problem
def binary_tournament(pop, P, _, **kwargs):
# The P input defines the tournaments and competitors
n_tournaments, n_competitors = P.shape
if n_competitors != 2:
raise Exception("Only pressure=2 allowed for binary tournament!")
# the result this function returns
import numpy as np
S = np.full(n_tournaments, -1, dtype=np.int)
# now do all the tournaments
for i in range(n_tournaments):
a, b = P[i]
# if the first individual is better, choose it
if pop[a].F < pop[b].F:
S[i] = a
# otherwise take the other individual
else:
S[i] = b
return S
selection = TournamentSelection(pressure=2, func_comp=binary_tournament)
problem = get_problem("rastrigin")
algorithm = GA(pop_size=100, eliminate_duplicates=True)
res = minimize(problem, algorithm, termination=('n_gen', 100), verbose=False)
print(res.X)2.2.3 Crossover
Crossover モジュールでは以下の5種類の突然変異方式を指定可能です。
Simulated Binary Crossover (SBX)
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.individual import Individual
from pymoo.core.problem import Problem
from pymoo.operators.crossover.sbx import SBX
def show(eta_cross):
problem = Problem(n_var=1, xl=0.0, xu=1.0)
a, b = Individual(X=np.array([0.2])), Individual(X=np.array([0.8]))
parents = [[a, b] for _ in range(5000)]
off = SBX(prob=1.0, prob_var=1.0, eta=eta_cross).do(problem, parents)
Xp = off.get("X")
plt.hist(Xp, range=(0, 1), bins=200, density=True, color="red")
plt.show()
show(1)Point Crossover
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.individual import Individual
from pymoo.core.problem import Problem
from pymoo.operators.crossover.pntx import PointCrossover, SinglePointCrossover, TwoPointCrossover
n_var, n_matings = 50, 30
problem = Problem(n_var=n_var, xl=0.0, xu=1.0, var_type=int)
a, b = Individual(X=np.arange(1, n_var + 1)), Individual(X=-np.arange(1, n_var + 1))
parents = [[a, b] for _ in range(n_matings)]
def show(M):
plt.figure(figsize=(4, 6))
plt.imshow(M, cmap='Greys', interpolation='nearest')
plt.xlabel("Variables")
plt.ylabel("Individuals")
plt.show()
print("One Point Crossover")
off = SinglePointCrossover(prob=1.0).do(problem, parents)
Xp = off.get("X")
show(Xp[:n_matings] != a.X)
print("Two Point Crossover")
off = TwoPointCrossover(prob=1.0).do(problem, parents)
Xp = off.get("X")
show(Xp[:n_matings] != a.X)
print("K Point Crossover (k=4)")
off = PointCrossover(prob=1.0, n_points=4).do(problem, parents)
Xp = off.get("X")
show(Xp[:n_matings] != a.X)Exponential Crossover
from pymoo.operators.crossover.expx import ExponentialCrossover
off = ExponentialCrossover(prob=1.0, prob_exp=0.9).do(problem, parents)
Xp = off.get("X")
show((Xp[:n_matings] != a.X))Uniform Crossover
from pymoo.operators.crossover.ux import UniformCrossover
off = UniformCrossover(prob=1.0).do(problem, parents)
Xp = off.get("X")
show(Xp[:n_matings] != a.X)Half Uniform Crossover (‘bin_hux’, ‘int_hux’)
from pymoo.operators.crossover.hux import HalfUniformCrossover
n_var, n_matings = 100, 100
problem = Problem(n_var=n_var, xl=0.0, xu=1.0, var_type=int)
a = Individual(X=np.full(n_var, False))
b = Individual(X=np.array([k % 5 == 0 for k in range(n_var)]))
parents = [[a, b] for _ in range(n_matings)]
off = HalfUniformCrossover(prob=1.0).do(problem, parents)
Xp = off.get("X")
show(Xp[:n_matings] != a.X)
diff_a_to_b = (a.X != b.X).sum()
diff_a_to_off = (a.X != Xp[:n_matings]).sum()
print("Difference in bits (a to b): ", diff_a_to_b)
print("Difference in bits (a to off): ", diff_a_to_off)
print("Crossover Rate: ", diff_a_to_off / diff_a_to_b)2.2.4 Mutation
Mutation モジュールでは以下の2種類の突然変異方式を指定可能です。
Polynomial Mutation (PM)
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.population import Population
from pymoo.core.problem import Problem
from pymoo.operators.mutation.pm import PolynomialMutation
def show(eta_mut):
problem = Problem(n_var=1, xl=0.0, xu=1.0)
X = np.full((5000, 1), 0.5)
pop = Population.new(X=X)
mutation = PolynomialMutation(prob=1.0, eta=eta_mut)
off = mutation(problem, pop)
Xp = off.get("X")
plt.hist(Xp, range=(0.0, 1.0), bins=200, density=True, color="red")
plt.show()
show(30)Bitflip Mutation (BM)
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.population import Population
from pymoo.core.problem import Problem
from pymoo.operators.mutation.bitflip import BitflipMutation
n_var, n_matings = 100, 50
problem = Problem(n_var=n_var, vtype=bool)
X = np.full((100, 100), False)
pop = Population.new(X=X)
mutation = BitflipMutation(prob=0.5, prob_var=0.3)
Xp = mutation(problem, pop).get("X")
plt.figure(figsize=(4, 4))
plt.imshow(X != Xp, cmap='Greys', interpolation='nearest')
plt.show()2.2 差分進化法(DE: Differential Evolution)
続いて差分進化法です。こちらも単目的最適化を想定して作られています。
from pymoo.algorithms.soo.nonconvex.de import DE
from pymoo.factory import get_problem
from pymoo.operators.sampling.lhs import LHS
from pymoo.optimize import minimize
problem = get_problem("ackley", n_var=10)
algorithm = DE(
pop_size=100,
sampling=LHS(),
variant="DE/rand/1/bin",
CR=0.5,
F=0.3,
dither="vector",
jitter=False
)
res = minimize(problem,
algorithm,
seed=1,
verbose=False)
print("Best solution found: \nX = %s\nF = %s" % (res.X, res.F))| 主な引数 | 説明 |
| pop_size | 集団サイズ(整数) |
| sampling | 初期集団のサンプリング方法 (2.2.1項参照) |
| variant | DEの種類。DE/x/y/zとして x: perturbation個体の選択方式 (rand/best) y: 差分ベクトルの数 z: 交叉の種類 (bin/exp) {DE/rand/1/bin}が一般的 |
| F | 交叉に使用される重み (float) |
| CR | 個体がdonor vectorからの変数を交換する確率 (float) |
| dither | {'no','scalar','vector'}'scalar':1世代で同じditherを使用'vector':各個体に対して異なるditherを使用 |
| jitter | 適応的にFを変化させるか否か (bool) Trueの場合,乱数的に小さな値が加減される |
2.3 粒子群最適化(PSO: Particle Swarm Optimization)
PSOです。単目的最適化を想定しています。
from pymoo.algorithms.soo.nonconvex.pso import PSO
from pymoo.factory import get_problem
from pymoo.operators.sampling.lhs import LHS
from pymoo.optimize import minimize
problem = get_problem("ackley", n_var=10)
algorithm = PSO(
pop_size=25,
sampling=LHS(),
adaptive = True,
w = 0.9,
c1 = 2.0,
c2 = 2.0,
initial_velocity = "random",
max_velocity_ratio = 0.20,
pertube_best = True,
)
res = minimize(problem,
algorithm,
seed=1,
verbose=False)
print("Best solution found: \nX = %s\nF = %s" % (res.X, res.F))| 主な引数 | 説明 |
| pop_size | 集団サイズ (int) |
| sampling | 初期集団のサンプリング方法(2.2.1項参照) |
| adaptive | w, c1, c2を動的に変化するか(bool) |
| w | 速度更新式の前速度項の重み(慣性)(float) |
| c1 | 速度更新式の係数 (float) |
| c2 | 速度更新式の係数 (float) |
| initial_velocity | 各粒子の初速の割り当て方法 (‘random’/’zero’) |
| max_velocity_rate | 最大速度の割合 (float) |
| pertube_best | (bool) |
2.4 NSGA-II (Non-dominated Sorting Genetic Algorithm)
NSGA-IIです。ここから多目的最適化です。
from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.factory import get_problem
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter
problem = get_problem("zdt1")
algorithm = NSGA2(pop_size=100)
res = minimize(problem,
algorithm,
('n_gen', 200),
seed=1,
verbose=False)
plot = Scatter()
plot.add(problem.pareto_front(), plot_type="line", color="black", alpha=0.7)
plot.add(res.F, color="red")
plot.show()| 主な引数 | 説明 |
| pop_size | 集団サイズ (int) |
| sampling | 初期集団のサンプリング方法(2.2.1項参照) |
| selection | 選択(2.2.2項参照) |
| crossover | 交叉(2.2.3項参照) |
| mutation | 突然変異(2.2.4項参照) |
| eliminate_duplicates | 親と子の集団内での重複を排除するか (bool) |
| n_offsprings | 交配によって作られる子孫の数 (int) デフォルトは集団サイズ |
2.5 R-NSGA-II
NSGA-IIの生存選択を修正したアルゴリズムです。reference pointsを設定し,その点に近い個体ほど生存しやすくなります。
import numpy as np
from pymoo.algorithms.moo.rnsga2 import RNSGA2
from pymoo.factory import get_problem
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter
problem = get_problem("zdt1", n_var=30)
pf = problem.pareto_front()
ref_points = np.array([[0.5, 0.2], [0.1, 0.6]])
algorithm = RNSGA2(
ref_points=ref_points,
pop_size=40,
epsilon=0.01,
normalization='front',
extreme_points_as_reference_points=False,
weights=np.array([0.5, 0.5]))
res = minimize(problem,
algorithm,
save_history=True,
termination=('n_gen', 250),
seed=1,
pf=pf,
disp=False)
Scatter().add(pf, label="pf").add(res.F, label="F").add(ref_points, label="ref_points").show()| 主な引数 | 説明 |
| ref_points | 基準点 (numpy.array) |
| epsilon | (float) |
| weights | (numpy.array) |
| normalization | (‘no’/’front’/’ever’) |
| extreme_points_as _reference_points |
(bool) |
| pop_size | 集団サイズ (int) |
| sampling | 初期集団のサンプリング方法(2.2.1項参照) |
| selection | 選択(2.2.2項参照) |
| crossover | 交叉(2.2.3項参照) |
| mutation | 突然変異(2.2.4項参照) |
| eliminate_duplicates | 親と子の集団内での重複を排除するか (bool) |
| n_offsprings | 交配によって作られる子孫の数 (int) デフォルトは集団サイズ |
2.6 NSGA-III
NSGA-IIIです。NSGA-IIに比べて,目的変数が高次元の場合でも高い収束性を実現できます。
from pymoo.algorithms.moo.nsga3 import NSGA3
from pymoo.problems import get_problem
from pymoo.util.ref_dirs import get_reference_directions
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter
ref_dirs = get_reference_directions("das-dennis", 3, n_partitions=12)
algorithm = NSGA3(pop_size=92,
ref_dirs=ref_dirs)
res = minimize(get_problem("dtlz1"),
algorithm,
seed=1,
termination=('n_gen', 600))
Scatter().add(res.F).show()| 主な引数 | 説明 |
| ref_dirs | 最適化で使用する基準方向 (numpy.array) (2.6.1項参照) |
| pop_size | 集団サイズ (int) |
| sampling | 初期集団のサンプリング方法(2.2.1項参照) |
| selection | 選択(2.2.2項参照) |
| crossover | 交叉(2.2.3項参照) |
| mutation | 突然変異(2.2.4項参照) |
| eliminate_duplicates | 親と子の集団内での重複を排除するか (bool) |
| n_offsprings | 交配によって作られる子孫の数 (int) デフォルトは集団サイズ |
2.6.1 Reference Direction
進化的多目的最適化アルゴリズムにおいて設定が必要な Reference Direction として,pymoo では Das-Dennis,Riesz s-Energy,Multi-layer Approach の3種類の設定方法が実装されています。これらの理論的背景はドキュメントや原論文を参照してください。
・Das-Dennis
from pymoo.visualization.scatter import Scatter
from pymoo.util.ref_dirs import get_reference_directions
ref_dirs = get_reference_directions(
"das-dennis",
3, # 次元
n_partitions=12 # 分割数
)
Scatter().add(ref_dirs).show()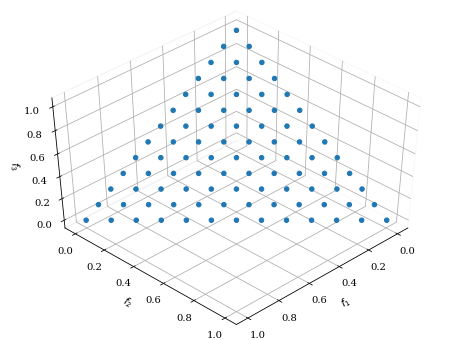
点の数は以下の式に基づいて計算されます。ただし,M は次元,p は n_partitions です。
$$_{M+p-1} C_p=\frac{(M+p-1)\times (M+p-2)\times \cdots \times M}{p\times (p-1) \times \cdots \times 1}$$
・Riesz s-Energy
from pymoo.visualization.scatter import Scatter
from pymoo.util.ref_dirs import get_reference_directions
ref_dirs = get_reference_directions(
"energy",
3, # 次元
90, # 点の数
seed=1, # 乱数シード
)
Scatter().add(ref_dirs).show()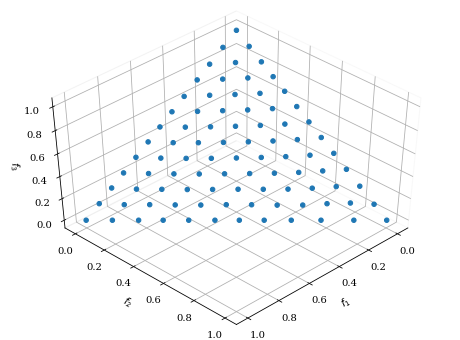
・Multi-layer Approach
このアプローチでは,生成点の偏りを表現することができます。これには,次元や分割数の他に,対応するスケーリング scaling を設定する必要があります。
from pymoo.visualization.scatter import Scatter
from pymoo.util.ref_dirs import get_reference_directions
ref_dirs = get_reference_directions(
"multi-layer",
get_reference_directions("das-dennis", 3, n_partitions=12, scaling=1.0),
get_reference_directions("das-dennis", 3, n_partitions=12, scaling=0.5)
)
Scatter().add(ref_dirs).show()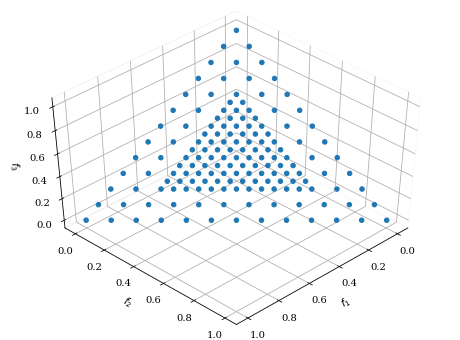
スケーリングの設定を必要としない方法として,Riesz s-Energy 法をスケーリング値の最適化に用いる方法も実装されています。
from pymoo.visualization.pcp import PCP
from pymoo.util.ref_dirs import get_reference_directions
partitions = [3, 2, 1, 1]
ref_dirs = get_reference_directions("layer-energy", 8, partitions)
PCP().add(ref_dirs).show()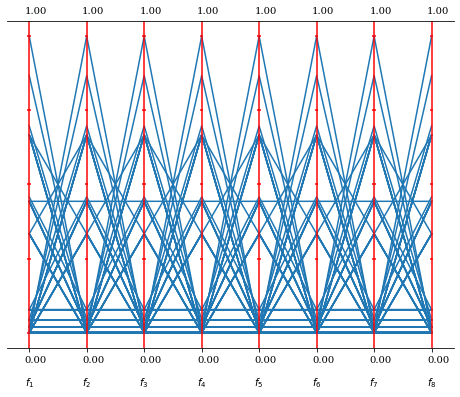
2.7 U-NSGA-III
NSGA-IIIの改良版です。Uは unified の略で,トーナメント圧 (tournament pressure) を導入して特性を向上しています。目的変数の次元が1,2の場合に特に高い収束性を示します。
import numpy as np
from pymoo.algorithms.moo.unsga3 import UNSGA3
from pymoo.problems import get_problem
from pymoo.optimize import minimize
problem = get_problem("ackley", n_var=30)
ref_dirs = np.array([[1.0]])
algorithm = UNSGA3(ref_dirs, pop_size=100)
res = minimize(problem,
algorithm,
termination=('n_gen', 150),
save_history=True,
seed=1)
print("UNSGA3: Best solution found: \nX = %s\nF = %s" % (res.X, res.F))| 主な引数 | 説明 |
| ref_dirs | 最適化で使用する基準方向 (numpy.array) (2.6.1項参照) |
| pop_size | 集団サイズ (int) |
| sampling | 初期集団のサンプリング方法(2.2.1項参照) |
| selection | 選択(2.2.2項参照) |
| crossover | 交叉(2.2.3項参照) |
| mutation | 突然変異(2.2.4項参照) |
| eliminate_duplicates | 親と子の集団内での重複を排除するか (bool) |
| n_offsprings | 交配によって作られる子孫の数 (int) デフォルトは集団サイズ |
2.8 R-NSGA-III
R-NSGA-IIIはR-NSGA-IIと同様に,NSGA-IIIの生存戦略を修正したアルゴリズムです。
import numpy as np
from pymoo.algorithms.moo.rnsga3 import RNSGA3
from pymoo.factory import get_problem
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter
problem = get_problem("zdt1")
pf = problem.pareto_front()
# Define reference points
ref_points = np.array([[0.3, 0.4], [0.8, 0.5]])
# Get Algorithm
algorithm = RNSGA3(
ref_points=ref_points,
pop_per_ref_point=50,
mu=0.1)
res = minimize(problem,
algorithm=algorithm,
termination=('n_gen', 300),
pf=pf,
seed=1,
verbose=False)
reference_directions = res.algorithm.survival.ref_dirs
plot = Scatter()
plot.add(pf, label="pf")
plot.add(res.F, label="F")
plot.add(ref_points, label="ref_points")
plot.add(reference_directions, label="ref_dirs")
plot.show()| 主な引数 | 説明 |
| ref_points | 基準点 (numpy.array) |
| pop_per_ref_point | 各基準点で使用する集団サイズ (int) |
| mu | 生存選択で使用する基準線のスケール (float) muが大きいと得られる解空間が広くなる |
| pop_size | 集団サイズ (int) |
| sampling | 初期集団のサンプリング方法(2.2.1項参照) |
| selection | 選択(2.2.2項参照) |
| crossover | 交叉(2.2.3項参照) |
| mutation | 突然変異(2.2.4項参照) |
| eliminate_duplicates | 親と子の集団内での重複を排除するか (bool) |
| n_offsprings | 交配によって作られる子孫の数 (int) デフォルトは集団サイズ |
2.9 BRKGA (Biased Random Key Genetic Algorithm)
組み合わせ問題で良く知られるBRKGAです。単目的最適化を想定しています。
import numpy as np
from pymoo.core.problem import ElementwiseProblem
from pymoo.core.duplicate import ElementwiseDuplicateElimination
from pymoo.algorithms.soo.nonconvex.brkga import BRKGA
from pymoo.optimize import minimize
class MyProblem(ElementwiseProblem):
def __init__(self, my_list):
self.correct = np.argsort(my_list)
super().__init__(n_var=len(my_list), n_obj=1, n_ieq_constr=0, xl=0, xu=1)
def _evaluate(self, x, out, *args, **kwargs):
pheno = np.argsort(x)
out["F"] = - float((self.correct == pheno).sum())
out["pheno"] = pheno
out["hash"] = hash(str(pheno))
class MyElementwiseDuplicateElimination(ElementwiseDuplicateElimination):
def is_equal(self, a, b):
return a.get("hash") == b.get("hash")
np.random.seed(2)
list_to_sort = np.random.random(20)
problem = MyProblem(list_to_sort)
print("Sorted by", np.argsort(list_to_sort))
algorithm = BRKGA(
n_elites=200,
n_offsprings=700,
n_mutants=100,
bias=0.7,
eliminate_duplicates=MyElementwiseDuplicateElimination())
res = minimize(problem,
algorithm,
("n_gen", 75),
seed=1,
verbose=False)
print("Best solution found: \nX = %s\nF = %s" % (res.X, res.F))
print("Solution", res.opt.get("pheno")[0])
print("Optimum ", np.argsort(list_to_sort))
print("Best solution found: \nX = %s\nF = %s" % (res.X, res.F))
print("Solution", res.opt.get("pheno")[0])
print("Optimum ", np.argsort(list_to_sort))| 主な引数 | 説明 |
| n_elites | エリート個体の数 (int) |
| n_offsprings | 子孫の数 (int) |
| n_mutants | 世代ごとに導入する変異の数 (int) |
| bias | 子孫がエリート親の対立遺伝子を受け継ぐことによるバイアス (float) |
| eliminate_duplicates | 親と子の集団内での重複を排除するか (bool) |
2.10 Nelder-Mead法
Nelder-Mead法です。単目的最適化を想定しています。
from pymoo.algorithms.soo.nonconvex.nelder import NelderMead
from pymoo.problems import get_problem
from pymoo.optimize import minimize
problem = get_problem("sphere")
algorithm = NelderMead()
res = minimize(problem,
algorithm,
seed=1,
verbose=False)
print("Best solution found: \nX = %s\nF = %s" % (res.X, res.F))| 主な引数 | 説明 |
| X | 探索の基準となる初期点 (np.array/Population) デフォルトはNoneで,ランダムな点から開始する |
| func_params | 探索のためのパラメータを返す関数 (func) デフォルトでは以下 |
| criterion_local_restart | ローカルリスタートを行うかどうか (Termination) |
2.11 Hooke-Jeevesパターン探索法
パターン探索です。こちらも単目的最適化を想定しています。
from pymoo.algorithms.soo.nonconvex.pattern import PatternSearch
from pymoo.factory import get_problem
from pymoo.optimize import minimize
problem = get_problem("ackley", n_var=30)
algorithm = PatternSearch()
res = minimize(problem,
algorithm,
seed=1,
verbose=False)
print("Best solution found: \nX = %s\nF = %s" % (res.X, res.F))| 主な引数 | 説明 |
| x0 | 初期探索点 (numpy.array) 指定しない場合はラテン超方格法で生成される |
| n_sample_points | 初期探索点の数 (int) x0が指定されていない場合に使用 |
| explr_delta | 探索移動に使用される値(割合) (float) |
| explr_rho | 探索移動が失敗した場合にdeltaに乗じる係数 (float) |
| pattern_step | 新しい中心点へのステップの大きさ (float) |
| eps | 追加の終了基準 (float) 全てのdeltaがepsilonより小さい場合,終了する |
2.12 CMA-ES (Covariance Matrix Adaptation Evolution Strategy)
CMA-ESです。単目的最適化を想定しています。
from pymoo.algorithms.soo.nonconvex.cmaes import CMAES
from pymoo.problems import get_problem
from pymoo.optimize import minimize
problem = get_problem("sphere")
algorithm = CMAES()
res = minimize(problem,
algorithm,
seed=1,
verbose=False)
print(f"Best solution found: \nX = {res.X}\nF = {res.F}\nCV= {res.CV}")CMA-ESには既にいくつかの停止基準が実装されています。
res = minimize(problem,
algorithm,
('n_iter', 10),
seed=1,
verbose=True)
print("Best solution found: \nX = %s\nF = %s" % (res.X, res.F))res = minimize(problem,
algorithm,
('n_evals', 50),
seed=1,
verbose=True)
print("Best solution found: \nX = %s\nF = %s" % (res.X, res.F))また,簡単にリスタートを行うことが可能です。
problem = get_problem("rastrigin")
algorithm = CMAES(restarts=10, restart_from_best=True)
res = minimize(problem,
algorithm,
('n_evals', 2500),
seed=1,
verbose=False)
print("Best solution found: \nX = %s\nF = %s" % (res.X, res.F))内部的にcma.fmin2関数を呼び出して,探索の初期値を選択することも可能です。
import numpy as np
from pymoo.util.normalization import denormalize
# define an intitial point for the search
np.random.seed(1)
x0 = denormalize(np.random.random(problem.n_var), problem.xl, problem.xu)
algorithm = CMAES(x0=x0,
sigma=0.5,
restarts=2,
maxfevals=np.inf,
tolfun=1e-6,
tolx=1e-6,
restart_from_best=True,
bipop=True)
res = minimize(problem,
algorithm,
seed=1,
verbose=False)
print("Best solution found: \nX = %s\nF = %s" % (res.X, res.F))※パラメータが多すぎて検証できておらず,ほぼ直訳です。
※こちらも参照してください。
| 主な引数 | 説明 |
| x0 | 最小解の初期推定値 list/numpy.array) |
| sigma | 各座標の初期標準偏差 (float) 探索領域幅の約1/4程度が推奨値 |
| parallelize | 目的関数を各評価ごとに呼び出すか否か (bool) |
| restarts | リスタートの回数 (int) 異なる点からリスタートする場合はx0を文字列で渡す |
| restart_from_best | 最適解からリスタートするか否か (bool) |
| incpopsize | リスタート前に集団サイズを増加するための乗数 (int) |
| eval_initial_x | 初期解を評価するか否か (bool) |
| noise_handler | NoiseHandlerクラス (class) |
| noise_change_sigma_exponent | NoiseHandlerのsigma増分の指数 (int) |
| noise_kappa_exponent | 再評価の代わりに,評価数をkappaとして使用 (int) |
| bipop | 母集団サイズの小/大を切り替えるパラメータ (bool) |
| AdaptSigma | (True) |
| CMA_active | 通常の更新後に行うnegative update (True) |
| CMA_activefac | 学習率の倍率 (1) |
| CMA_cmean | mean の学習率 (1) |
| CMA_const_trace | 正規化トレース (True/”arithm”/”geom”/”aeig”/”geig”) |
| CMA_diagonal | 対角線上の共分散行列での反復回数 (0*100*N/popsize**0.5) |
| CMA_eigenmethod | np.linalg.eigh/cma.utilities.math.eig/ pygsl.eigen.eigenvectors |
| CMA_elitist | エリート選択を行うか否か (bool/”initial”) |
| CMA_injections_ threshold_keep_len |
マハラノビス長が閾値以下であれば長さを維持 (0) |
| CMA_mirrors | 0.5未満は端数,1以上は数値として解釈,それ以外は0.16を使用 (popsize<6) |
| CMA_mirrormethod | 0:条件なし,1:選択,2:遅延を伴う選択 |
| CMA_mu | 親の選択パラメータ (None) |
| CMA_on | 全ての共分散行列の更新に対する乗数 (1) |
| CMA_sampler | cma.interfaces. StatisticalModelSamplerWithZeroMeanBaseClass |
| CMA_sampler_options | CMA_samplerのクラスのinitに引数として渡される選択肢 (dict) |
| CMA_rankmu | 共分散行列のrank-mu更新学習率の乗数 (1.0) |
| CMA_rankone | 共分散行列のランク1更新学習率の乗数 (1.0) |
| CMA_recombination_weights | CMA_muとpopsizeオプションを上書き (None) |
| CMA_dampsvec_fac | sigmaベクトルの更新のダンピング (np.inf) |
| CMA_dampsvec_fade | sigmaベクトルの更新のfade outパラメータ (0.1) |
| CMA_teststds | Cの非等方性初期分布のための係数 (None) |
| CMA_stds | 各座標におけるsigma0の乗数 (None) |
| CSA_dampfac | ステップサイズ減衰のための正の乗数 (1) |
| CSA_damp_mueff_exponent | 0にすると減衰がmueffに依存しないことを意味 (0.5) |
| CSA_disregard_length | Trueは未検証でそれぞれのパラメータも変更される (False) |
| CSA_clip_length_value | [0,0]は長さがN**0.5,[-1,1]は+-N/(N+2),など (None) |
| CSA_squared | シグマ適用には長さの二乗を使用 (False) |
| BoundaryHandler | BoundTransform or BoundPenalty, bounds in (None, [None, None])では使用しない |
| conditioncov_alleviate | 座標や主軸の状態の緩和に使用 ([1e8, 1e12]) |
| eval_final_mean | 戻り値の候補である最終平均値を評価 (True) |
| fixed_variables | 最適化されていないインデックスと値のペア (None) |
| ftarget | 目標関数値,最小化 (-inf) |
| integer_variables | インデックスリスト,標準偏差が小さくなりすぎるのを防ぐ ([]) |
| maxfevals | 関数評価の最大数 (inf) |
| maxiter | 最大反復回数 (100+150*(N+3)**2//popsize**0.5) |
| mean_shift_line_samples | 前回の平均値シフトと同列の2つの新しい解をサンプル (False) |
| mindx | 任意方向の標準偏差の最小値 (0) |
| minstd | 任意の座標方向での標準偏差の最小値 (0) |
| maxstd | 任意の座標方向での標準偏差の最大値 (inf) |
| pc_line_samples | 進化に沿ったラインの1サンプル (False) |
| popsize | 母集団の大きさ (4+int(3*np.log(N))) |
| randn | np.random.randn |
| signals_filename | cma_signals.in # (None) |
| termination_callback | 終了時にTrueを返す関数 (None) |
| timeout | 超えると停止するタイムアウト秒数 (inf) |
| tolconditioncov | 共分散行列の条件がtolconditioncov以上であれば停止 (1e14) |
| tolfacupx | ステップサイズがtolfacupxより大きくなると停止 (1e3) |
| tolupsigma | わずかな改善を伴うクリーピング動作を示す (1e20) |
| tolfun | 終了基準:関数値の許容範囲 (1e-11) |
| tolfunhist | 終了基準:関数値の履歴の許容範囲 (1e-12) |
| tolstagnation | 終了基準:関数値の履歴の許容範囲 (int(100+100*N**1.5/popsize)) |
| tolx | 終了基準:xの許容範囲 (1e-11) |
| typical_x | scaling_of_variablesで使用 (None) |
| updatecovwait | 分布の更新がない反復回数 (None) |
| cmaes_verbose | verbosity (3) |
| verb_append | 初期評価カウンター (0) |
| verb_disp | verb_dispのiterationごとにコンソール出力を表示する (100) |
| verb_flinameprefix | 出力パスとファイル名の接頭辞 (str) |
| verb_log | verb_logのiterationごとにデータを書き込む (1) |
| verb_plot | verb_plotのiterationごとにplot()を呼ぶ (0) |
| verb_time | 時間をコンソールに出力 (True) |
| vv | ハッキングのための汎用セット/dict, 値はself.opts[“vv”] (dict) |
| kwargs | 追加オプションを持つdict, cma.CMAOptions()参照 (dict) |
2.13 MOEA/D (Multiobjective Evolutionary Algorithm based on Decomposition)
MOEA/Dです。多目的最適化です。
from pymoo.algorithms.moo.moead import MOEAD
from pymoo.optimize import minimize
from pymoo.problems import get_problem
from pymoo.util.ref_dirs import get_reference_directions
from pymoo.visualization.scatter import Scatter
problem = get_problem("dtlz2")
ref_dirs = get_reference_directions("uniform", 3, n_partitions=12)
algorithm = MOEAD(
ref_dirs,
n_neighbors=15,
prob_neighbor_mating=0.7,
)
res = minimize(problem,
algorithm,
('n_gen', 200),
seed=1,
verbose=False)
Scatter().add(res.F).show()2.14 C-TAEA
C-TAEAです。多目的最適化です。
from pymoo.algorithms.moo.ctaea import CTAEA
from pymoo.problems import get_problem
from pymoo.util.ref_dirs import get_reference_directions
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter
problem = get_problem("c1dtlz1", None, 3, k=5)
ref_dirs = get_reference_directions("das-dennis", 3, n_partitions=12)
# create the algorithm object
algorithm = CTAEA(ref_dirs=ref_dirs)
# execute the optimization
res = minimize(problem,
algorithm,
('n_gen', 600),
seed=1,
verbose=False
)
sc = Scatter(legend=False, angle=(45, 30))
sc.add(problem.pareto_front(ref_dirs), plot_type='surface', alpha=0.2, label="PF", color="blue")
sc.add(res.F, facecolor="none", edgecolor="red")
sc.show()
3. 終了条件の定義
終了条件が指定されない場合,デフォルトの設定は下記のようになっています。
多目的最適化の場合。
from pymoo.termination.default import DefaultMultiObjectiveTermination
termination = DefaultMultiObjectiveTermination(
xtol=1e-8,
cvtol=1e-6,
ftol=0.0025,
period=30,
n_max_gen=1000,
n_max_evals=100000
)単目的最適化の場合。
from pymoo.termination.default import DefaultSingleObjectiveTermination
termination = DefaultSingleObjectiveTermination(
xtol=1e-8,
cvtol=1e-6,
ftol=1e-6,
period=20,
n_max_gen=1000,
n_max_evals=100000
)終了条件を指定する場合は,get_termination関数を用いて設定します。
from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.problems import get_problem
from pymoo.termination import get_termination
from pymoo.optimize import minimize
problem = get_problem("zdt3")
algorithm = NSGA2(pop_size=100)
termination = get_termination("n_eval", 300)
res = minimize(problem,
algorithm,
termination,
pf=problem.pareto_front(),
seed=1,
verbose=True)| 主な引数 | 説明 |
| n_eval | 評価回数の上限値 (int) |
| n_gen/n_iter | 世代/iterationの上限値 (int) |
| time | 実行時間の上限値 (str) 1時間30分の場合: get_termination("time", "01:30:00") |
| x_tol/xtol | 入力変数に基づく停止条件 |
| f_tol/ftol | 目的関数に基づく停止条件 |
xtolやftolに関しては,別に用意されている関数を用いて設定することを推奨されています。
xtolの場合
from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.problems import get_problem
from pymoo.optimize import minimize
from pymoo.termination.xtol import DesignSpaceTermination
from pymoo.termination.robust import RobustTermination
problem = get_problem("zdt3")
algorithm = NSGA2(pop_size=100)
termination = RobustTermination(DesignSpaceTermination(tol=0.01), period=20)
res = minimize(problem,
algorithm,
termination,
pf=problem.pareto_front(),
seed=1,
verbose=False)
print(res.algorithm.n_gen)ftolの場合
from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.problems import get_problem
from pymoo.optimize import minimize
from pymoo.termination.ftol import MultiObjectiveSpaceTermination
from pymoo.visualization.scatter import Scatter
problem = get_problem("zdt3")
algorithm = NSGA2(pop_size=100)
termination = RobustTermination(
MultiObjectiveSpaceTermination(tol=0.005, n_skip=5), period=20)
res = minimize(problem,
algorithm,
termination,
pf=True,
seed=1,
verbose=False)
print("Generations", res.algorithm.n_gen)
plot = Scatter(title="ZDT3")
plot.add(problem.pareto_front(use_cache=False, flatten=False), plot_type="line", color="black")
plot.add(res.F, facecolor="none", edgecolor="red", alpha=0.8, s=20)
plot.show()| 主な引数 | 説明 |
| tol | 更新幅がtolより小さかったら終了 |
| n_last | 何世代分の更新幅を考えるか |
| n_max_gen | 最大世代数(予備設定) |
| n_max_evals | 最大評価数(予備設定) |
| nth_gen | 終了基準を計算するタイミング,10なら10世代ごとに計算 |
4. 最適化の実行
定義したアルゴリズムと終了基準で問題を解きます。pymooでは,最適化問題を解くためのインターフェースとして Functional Interface と Object Oriented Interface があります。
4.1 Functional Interface
Functional Interface は minimize 関数を使用します。基本的には minimize 関数を使用することをお勧めします。
戻り値は Result オブジェクト(4.1.3項参照)で,最適値などの属性を提供します。詳しい結果の扱い方は5章を参照してください。
from pymoo.optimize import minimize
res = minimize(problem,
algorithm,
termination,
seed=1,
save_history=True,
verbose=True)==========================================================================================
n_gen | n_eval | cv (min) | cv (avg) | igd | gd | hv
==========================================================================================
1 | 40 | 0.00000E+00 | 2.36399E+01 | 0.355456661 | 0.005362269 | 0.259340233
2 | 50 | 0.00000E+00 | 1.15486E+01 | 0.355456661 | 0.005362269 | 0.259340233
3 | 60 | 0.00000E+00 | 5.277918607 | 0.355456661 | 0.005362269 | 0.259340233
4 | 70 | 0.00000E+00 | 2.406068542 | 0.336177786 | 0.003791374 | 0.267747228
5 | 80 | 0.00000E+00 | 0.908316880 | 0.146187673 | 0.030825699 | 0.326821728
6 | 90 | 0.00000E+00 | 0.264746300 | 0.146187673 | 0.030825699 | 0.326821728
7 | 100 | 0.00000E+00 | 0.054063822 | 0.127166639 | 0.048434536 | 0.326821728
8 | 110 | 0.00000E+00 | 0.003060876 | 0.116635438 | 0.040756917 | 0.333328216
9 | 120 | 0.00000E+00 | 0.00000E+00 | 0.114104403 | 0.033780540 | 0.333467251
10 | 130 | 0.00000E+00 | 0.00000E+00 | 0.113905849 | 0.079757906 | 0.336916611
11 | 140 | 0.00000E+00 | 0.00000E+00 | 0.108326595 | 0.061746460 | 0.350973236
12 | 150 | 0.00000E+00 | 0.00000E+00 | 0.075994278 | 0.028407765 | 0.409709713
13 | 160 | 0.00000E+00 | 0.00000E+00 | 0.075900587 | 0.028006615 | 0.410363369
14 | 170 | 0.00000E+00 | 0.00000E+00 | 0.060504000 | 0.025567286 | 0.411662871
15 | 180 | 0.00000E+00 | 0.00000E+00 | 0.049446911 | 0.016289051 | 0.418530080
16 | 190 | 0.00000E+00 | 0.00000E+00 | 0.045458331 | 0.011383437 | 0.420489384
17 | 200 | 0.00000E+00 | 0.00000E+00 | 0.039469853 | 0.009911055 | 0.430486842
18 | 210 | 0.00000E+00 | 0.00000E+00 | 0.029430084 | 0.005849149 | 0.436066481
19 | 220 | 0.00000E+00 | 0.00000E+00 | 0.026914825 | 0.006440139 | 0.438071834
20 | 230 | 0.00000E+00 | 0.00000E+00 | 0.025819848 | 0.006597745 | 0.439045983
21 | 240 | 0.00000E+00 | 0.00000E+00 | 0.025538102 | 0.006092177 | 0.439313321
22 | 250 | 0.00000E+00 | 0.00000E+00 | 0.025430023 | 0.005831189 | 0.439357583
23 | 260 | 0.00000E+00 | 0.00000E+00 | 0.022907750 | 0.005325638 | 0.441118548
24 | 270 | 0.00000E+00 | 0.00000E+00 | 0.020729474 | 0.005408909 | 0.444667855
25 | 280 | 0.00000E+00 | 0.00000E+00 | 0.020685726 | 0.004700076 | 0.447352036
26 | 290 | 0.00000E+00 | 0.00000E+00 | 0.018021642 | 0.004673768 | 0.449131574
27 | 300 | 0.00000E+00 | 0.00000E+00 | 0.017734569 | 0.004981929 | 0.452104699
28 | 310 | 0.00000E+00 | 0.00000E+00 | 0.017256071 | 0.004906941 | 0.452453391
29 | 320 | 0.00000E+00 | 0.00000E+00 | 0.017099845 | 0.004821622 | 0.452586422
30 | 330 | 0.00000E+00 | 0.00000E+00 | 0.015604763 | 0.004715009 | 0.454343077
31 | 340 | 0.00000E+00 | 0.00000E+00 | 0.015494765 | 0.004509278 | 0.454689229
32 | 350 | 0.00000E+00 | 0.00000E+00 | 0.015494765 | 0.004509278 | 0.454689229
33 | 360 | 0.00000E+00 | 0.00000E+00 | 0.013269463 | 0.002882294 | 0.456133797
34 | 370 | 0.00000E+00 | 0.00000E+00 | 0.012326693 | 0.002872865 | 0.456726256
35 | 380 | 0.00000E+00 | 0.00000E+00 | 0.011929203 | 0.002718091 | 0.456859586
36 | 390 | 0.00000E+00 | 0.00000E+00 | 0.011452732 | 0.002668863 | 0.459103818
37 | 400 | 0.00000E+00 | 0.00000E+00 | 0.011187256 | 0.002467009 | 0.459278838
38 | 410 | 0.00000E+00 | 0.00000E+00 | 0.010961294 | 0.002442439 | 0.459731947
39 | 420 | 0.00000E+00 | 0.00000E+00 | 0.010982275 | 0.002847599 | 0.459564223
40 | 430 | 0.00000E+00 | 0.00000E+00 | 0.010485987 | 0.002833493 | 0.460033718
| 主な引数 | 説明 |
| problem | pymooで定義した最適化問題 (1章参照) |
| algorithm | 最適化に用いるアルゴリズム (2章参照) |
| termination | アルゴリズムの終了条件 (3章参照) |
| seed | 乱数シード (int) |
| verbose | 結果を出力するか (bool) |
| display | 結果表示形式の指定 (4.1.1項参照) |
| callback | 世代ごとに行う処理の指定 (4.1.2項参照) |
| save_history | 履歴を保存するか (bool) |
| copy_algorithm | Algorithm オブジェクトを最適化前にコピーするか (bool) |
| copy_termination | Termination オブジェクトを最適化前にコピーするか (bool) |
4.1.1 Display
minimize 関数は各世代ごとに最適化情報を出力しますが,Display クラスを指定することで出力情報を変更することができます。
import numpy as np
from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.problems import get_problem
from pymoo.optimize import minimize
from pymoo.util.display.column import Column
from pymoo.util.display.output import Output
class MyOutput(Output):
def __init__(self):
super().__init__()
self.x_mean = Column("x_mean", width=13)
self.x_std = Column("x_std", width=13)
self.columns += [self.x_mean, self.x_std]
def update(self, algorithm):
super().update(algorithm)
self.x_mean.set(np.mean(algorithm.pop.get("X")))
self.x_std.set(np.std(algorithm.pop.get("X")))
problem = get_problem("zdt2")
algorithm = NSGA2(pop_size=100)
res = minimize(problem,
algorithm,
('n_gen', 10),
seed=1,
output=MyOutput(),
verbose=True)=================================================
n_gen | n_eval | x_mean | x_std
=================================================
1 | 100 | 0.5001227728 | 0.2877408633
2 | 200 | 0.4525139169 | 0.2845368465
3 | 300 | 0.4123143496 | 0.2826460505
4 | 400 | 0.3624091800 | 0.2680576859
5 | 500 | 0.3237124952 | 0.2590762910
6 | 600 | 0.2743448091 | 0.2384785285
7 | 700 | 0.2565909842 | 0.2368465686
8 | 800 | 0.2294679740 | 0.2210448785
9 | 900 | 0.1929644605 | 0.1955969395
10 | 1000 | 0.1785042488 | 0.1927740079
詳細はこちら
4.1.2 Callback
minimize 関数内で世代ごとに追加の処理を行いたい場合,Callback クラスを指定します。結果に対する追加の計算やアルゴリズムオブジェクトの修正も行うことができます。
例として,各世代の最良解を追跡するクラスを指定します。
import matplotlib.pyplot as plt
import numpy as np
from pymoo.algorithms.soo.nonconvex.ga import GA
from pymoo.problems import get_problem
from pymoo.core.callback import Callback
from pymoo.optimize import minimize
class MyCallback(Callback):
def __init__(self) -> None:
super().__init__()
self.data["best"] = []
def notify(self, algorithm):
self.data["best"].append(algorithm.pop.get("F").min())
problem = get_problem("sphere")
algorithm = GA(pop_size=100)
res = minimize(problem,
algorithm,
('n_gen', 10),
seed=1,
callback=MyCallback(),
save_history=True,
verbose=True)
val = res.algorithm.callback.data["best"]
plt.plot(np.arange(len(val)), val)
plt.show()=============================================
n_gen | n_eval | fopt | favg
=============================================
1 | 100 | 0.387099336 | 0.831497479
2 | 200 | 0.302189349 | 0.578035582
3 | 300 | 0.267733594 | 0.443801185
4 | 400 | 0.188215259 | 0.347200983
5 | 500 | 0.083479177 | 0.272644726
6 | 600 | 0.083479177 | 0.212567874
7 | 700 | 0.072492126 | 0.173574163
8 | 800 | 0.051256476 | 0.140740462
9 | 900 | 0.041778020 | 0.110370322
10 | 1000 | 0.041778020 | 0.089125798
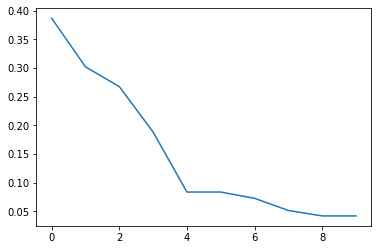
MyCallback クラス内の notify 関数では,各世代ごとに Algorithm オブジェクト内の情報を保存しています。指定可能な Algorithm オブジェクトの属性は5.2.1項を参照してください。
内容によっては,これらの処理を最適化計算の実行後に行うことも可能です。その場合,minimize 関数において save_history=True として履歴を保存しておく必要があります。(詳細は5.2.1項を参照してください。)
val = [e.pop.get("F").min() for e in res.history]
plt.plot(np.arange(len(val)), val)
plt.show()
4.1.3 Result
アルゴリズムが実行されると,Resultオブジェクトが返されます。Resultオブジェクトには,探索結果に関する情報を含みます。
| 変数 | 戻り値 |
| res.X | 最適解orパレート解の設計変数の値 |
| res.F | 最適解orパレート解の目的変数の値 |
| res.G | 制約条件の値 |
| res.CV | 制約違反の値 |
| res.algorithm | 使用した Algorithm オブジェクト |
| res.pop | 最終的な Population オブジェクト |
| res.history | Algorithm オブジェクトの履歴 ( save_history=True の場合) |
| res.time | アルゴリズムの実行時間 |
下記プログラムの例を示します。
from pymoo.algorithms.soo.nonconvex.ga import GA
from pymoo.problems import get_problem
from pymoo.optimize import minimize
problem = get_problem("sphere")
algorithm = GA(pop_size=5)
res = minimize(problem,
algorithm,
('n_gen', 30),
seed=1)結果はこのように格納されます。今回の設定では制約条件が存在しないため,res.G は None ,res.CV は0を出力します。
res.X, res.F, res.G, res.CV(array([0.38401994, 0.51096839, 0.51958345, 0.50705362, 0.64625327, 0.52972181, 0.51346167, 0.57393803, 0.48975355, 0.49213286]), array([0.04209328]), None, array([0.]))
res.algorithm, res.pop(&lt;pymoo.algorithms.so_genetic_algorithm.GA at 0x226966bb448 &gt;, Population([&lt;pymoo.model.individual.Individual object at 0x00000226966E9C08 &gt;, &lt;pymoo.model.individual.Individual object at 0x00000226966E99C8 &gt;, &lt;pymoo.model.individual.Individual object at 0x0000022695D930C8 &gt;, &lt;pymoo.model.individual.Individual object at 0x00000226966E9C48 &gt;, &lt;pymoo.model.individual.Individual object at 0x00000226966C0C08 &gt;], dtype=object))
最終的な母集団情報は,get メソッドにより抽出可能です。
res.pop.get("X"), res.pop.get("F")(array([[0.38401994, 0.51096839, 0.51958345, 0.50705362, 0.64625327, 0.52972181, 0.51346167, 0.57393803, 0.48975355, 0.49213286], [0.38401994, 0.51096839, 0.51958345, 0.50705362, 0.64625327, 0.52972181, 0.51346167, 0.57393803, 0.51785226, 0.49213286], [0.38401994, 0.51099826, 0.44223106, 0.50705362, 0.64625327, 0.52808581, 0.51346167, 0.57393803, 0.39462856, 0.49213286], [0.38401994, 0.51099826, 0.44223106, 0.50705362, 0.64625327, 0.52864113, 0.51346167, 0.57393803, 0.39462856, 0.49213286], [0.38401994, 0.47389685, 0.44223106, 0.50705362, 0.64625327, 0.52808581, 0.51346167, 0.57393803, 0.39462856, 0.49213286]]), array([[0.04209328], [0.04230699], [0.05595125], [0.05598275], [0.05651167]]))
4.2 Object Oriented Interface
オブジェクト指向のアプローチも可能です。nextメソッドを呼び出すことで,アルゴリズムを直接変更して実行することができます。
import copy
# アルゴリズムをコピー
obj = copy.deepcopy(algorithm)
# 問題設定
obj.setup(problem, termination=termination, seed=1)
# 終了基準が満たされるまで実行
while obj.has_next():
# アルゴリズムの反復
obj.next()
# 結果のプリント
print(f"gen: {obj.n_gen} n_nds: {len(obj.opt)} constr: {obj.opt.get('CV').min()} ideal: {obj.opt.get('F').min(axis=0)}")
# 結果を取得
result = obj.result()gen: 1 n_nds: 1 constr: 0.0 ideal: [0.38709934] gen: 2 n_nds: 1 constr: 0.0 ideal: [0.30218935] gen: 3 n_nds: 1 constr: 0.0 ideal: [0.26773359] gen: 4 n_nds: 1 constr: 0.0 ideal: [0.18821526] gen: 5 n_nds: 1 constr: 0.0 ideal: [0.08347918] gen: 6 n_nds: 1 constr: 0.0 ideal: [0.08347918] gen: 7 n_nds: 1 constr: 0.0 ideal: [0.07249213] gen: 8 n_nds: 1 constr: 0.0 ideal: [0.05125648] gen: 9 n_nds: 1 constr: 0.0 ideal: [0.04177802] gen: 10 n_nds: 1 constr: 0.0 ideal: [0.04177802] gen: 11 n_nds: 1 constr: 0.0 ideal: [0.03164457] gen: 12 n_nds: 1 constr: 0.0 ideal: [0.03005581] gen: 13 n_nds: 1 constr: 0.0 ideal: [0.02185533] gen: 14 n_nds: 1 constr: 0.0 ideal: [0.017621] gen: 15 n_nds: 1 constr: 0.0 ideal: [0.0147564] gen: 16 n_nds: 1 constr: 0.0 ideal: [0.0147564] gen: 17 n_nds: 1 constr: 0.0 ideal: [0.01297642] gen: 18 n_nds: 1 constr: 0.0 ideal: [0.00863792] gen: 19 n_nds: 1 constr: 0.0 ideal: [0.00639944] gen: 20 n_nds: 1 constr: 0.0 ideal: [0.00639944] gen: 21 n_nds: 1 constr: 0.0 ideal: [0.00526431] gen: 22 n_nds: 1 constr: 0.0 ideal: [0.00526431] gen: 23 n_nds: 1 constr: 0.0 ideal: [0.00395399] gen: 24 n_nds: 1 constr: 0.0 ideal: [0.00250103] gen: 25 n_nds: 1 constr: 0.0 ideal: [0.00250103] gen: 26 n_nds: 1 constr: 0.0 ideal: [0.00250103] gen: 27 n_nds: 1 constr: 0.0 ideal: [0.00250103] gen: 28 n_nds: 1 constr: 0.0 ideal: [0.00250103] gen: 29 n_nds: 1 constr: 0.0 ideal: [0.00250103] gen: 30 n_nds: 1 constr: 0.0 ideal: [0.00168171] gen: 31 n_nds: 1 constr: 0.0 ideal: [0.00168171] gen: 32 n_nds: 1 constr: 0.0 ideal: [0.00168171] gen: 33 n_nds: 1 constr: 0.0 ideal: [0.00168171] gen: 34 n_nds: 1 constr: 0.0 ideal: [0.00102891] gen: 35 n_nds: 1 constr: 0.0 ideal: [0.00102891] gen: 36 n_nds: 1 constr: 0.0 ideal: [0.00102891] gen: 37 n_nds: 1 constr: 0.0 ideal: [0.00096197] gen: 38 n_nds: 1 constr: 0.0 ideal: [0.00071648] gen: 39 n_nds: 1 constr: 0.0 ideal: [0.00033338] gen: 40 n_nds: 1 constr: 0.0 ideal: [0.00033338]
5. 結果の検討
5.1 Visualization
最適化結果を可視化するためには,Visualization に格納されているモジュールを使用します。
5.1.1 Scatter Plot (散布図)
2次元の散布図の場合,以下のようにプロットできます。
from pymoo.visualization.scatter import Scatter
from pymoo.problems import get_problem
F = get_problem("zdt3").pareto_front(use_cache=False, flatten=True)
plot = Scatter(legend=True)
plot.add(F, s=30, facecolors='none', edgecolors='r', label='red point')
plot.add(F, plot_type="line", color="black", linewidth=2, label='black line')
plot.show()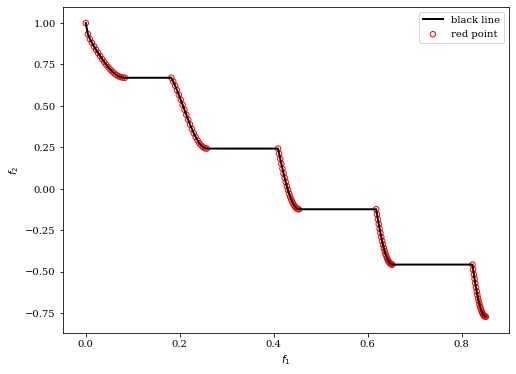
3次元の散布図の場合も同様です。
from pymoo.visualization.scatter import Scatter
from pymoo.problems import get_problem
from pymoo.util.ref_dirs import get_reference_directions
ref_dirs = get_reference_directions("uniform", 3, n_partitions=12)
F = get_problem("dtlz1").pareto_front(ref_dirs)
plot = Scatter()
plot.add(F)
plot.show()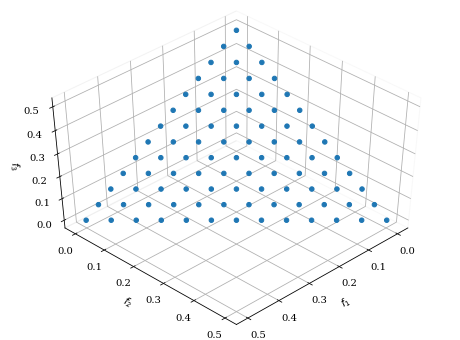
N次元の場合には,Pairwise Scatter Plots が利用可能です。
import numpy as np
from pymoo.visualization.scatter import Scatter
F = np.random.random((30, 4))
plot = Scatter(tight_layout=True)
plot.add(F, s=10)
plot.add(F[10], s=30, color="red")
plot.show()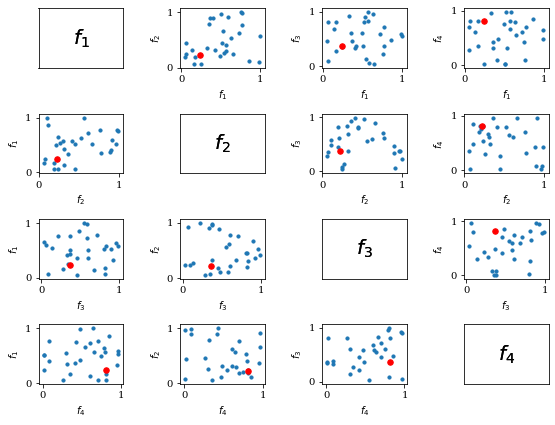
| 主な引数 | 説明 |
| axis_style | 軸スタイル(e.g. color, alpha…)(dict)* |
| endpoint_style | endpointのスタイル (dict)* |
| labels | 軸ラベル (str or list) |
| figsize | 図のサイズ (tuple) |
| title | 図のタイトル (str or tuple) |
| legend | 凡例を表示するか (bool) |
| tight_layout | サブプロット間を調節するか (bool) |
| cmap | カラーマップ (colormap) |
*axis_style, endpoint_style について,いろいろ検証を行いましたがスタイルが図に反映されません。ソースコードを見る限り,スタイル反映の箇所がないため,バグかと思います。
5.1.2 Parallel Coordinate Plots (平行座標プロット)
高次元データの場合,PCPはどのように解が分布しているかを分析できます。
from pymoo.problems import get_problem
from pymoo.util.ref_dirs import get_reference_directions
from pymoo.visualization.pcp import PCP
# データセットの作成,DTLZ1のパレートフロントをスケーリングしたもの
ref_dirs = get_reference_directions("das-dennis", 6, n_partitions=5) * [2, 4, 8, 16, 32, 64]
F = get_problem("dtlz1").pareto_front(ref_dirs)
PCP().add(F).show()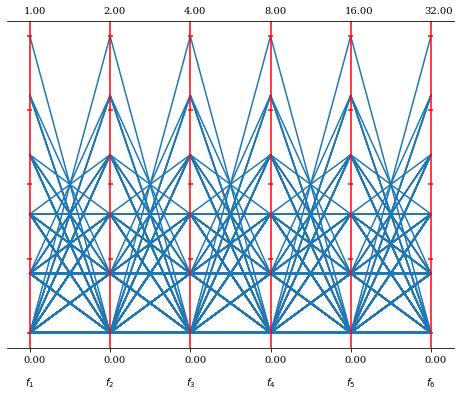
50番目と75番目の解を強調し,さらに付加情報を加える場合,例えばこのようにプログラムします。
from pymoo.problems import get_problem
from pymoo.util.ref_dirs import get_reference_directions
from pymoo.visualization.pcp import PCP
# データセットの作成,DTLZ1のパレートフロントをスケーリングしたもの
ref_dirs = get_reference_directions("das-dennis", 6, n_partitions=5) * [2, 4, 8, 16, 32, 64]
F = get_problem("dtlz1").pareto_front(ref_dirs)
plot = PCP()
plot.set_axis_style(color="grey", alpha=0.5)
plot.add(F, color="grey", alpha=0.3)
plot.add(F[50], linewidth=5, color="red")
plot.add(F[75], linewidth=5, color="blue")
plot.show()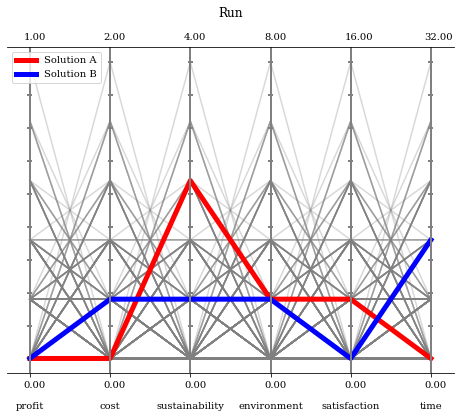
| 主な引数 | 説明 |
| bounds | 各軸の上下限値 (tuple/list/numpy.array) e.g. bounds=[[1,1,1,2,2,5],[32,32,32,32,32,32]] |
| axis_style | 軸スタイル(e.g. color, alpha…)(dict) |
| labels | 軸ラベル (str or list) |
| n_ticks | 目盛りの数 (int) |
| show_bounds | 上下限値を軸に表示するか (bool) |
| normalize_each_axis | 各軸を正規化するか (bool) |
| figsize | 図のサイズ (tuple) |
| title | 図のタイトル (str or tuple) |
| legend | 凡例を表示するか (bool) |
| tight_layout | サブプロット間を調節するか (bool) |
| cmap | カラーマップ (colormap) |
5.1.3 Heatmap
値の分布の把握には,ヒートマップが有効です。
デフォルトでは,大きな値は白,小さな値は青に設定されています。
import numpy as np
from pymoo.visualization.heatmap import Heatmap
np.random.seed(1234)
F = np.random.random((4, 6))
Heatmap().add(F).show()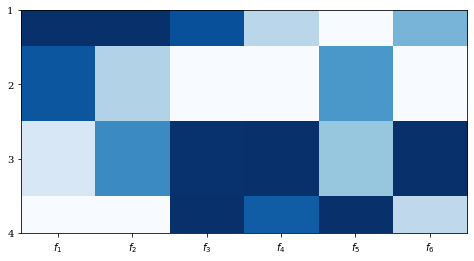
これまでと同様に,様々なカスタマイズが可能です。
import numpy as np
from pymoo.visualization.heatmap import Heatmap
np.random.seed(1234)
F = np.random.random((4, 6))
plot = Heatmap(title=("Optimization", {'pad': 15}),
cmap="Oranges_r",
solution_labels=["Solution A", "Solution B", "Solution C", "Solution D"],
labels=["profit", "cost", "sustainability", "environment", "satisfaction", "time"])
plot.add(F)
plot.show()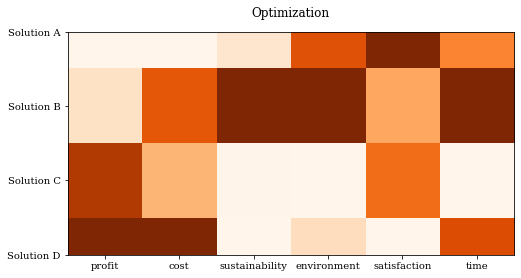
| 主な引数 | 説明 |
| order_by_objectives | 結果をz軸の値順に並べるかどうか (int or list) x軸のどれかを指定すると,y軸がz軸の値順にソートされる |
| reverse | True の場合,大きな値は白,小さな値は対応する色になる (bool) False の場合は逆 |
| solution_labels | 縦軸ラベル (bool or list) |
| bounds | 各軸の上下限値 (tuple/list/numpy.array) e.g. bounds=[[1,1,1,2,2,5],[32,32,32,32,32,32]] |
| labels | 横軸ラベル (str or list) |
| figsize | 図のサイズ (tuple) |
| title | 図のタイトル (str or tuple) |
| legend | 凡例を表示するか (bool) |
| tight_layout | サブプロット間を調節するか (bool) |
| cmap | カラーマップ (colormap) |
5.1.4 Petal Diagram
解ごとの目的関数の値を比較するには,ペタル図が有効です。
import numpy as np
from pymoo.visualization.petal import Petal
np.random.seed(1234)
F = np.random.random((1, 6))
print(F)
Petal(bounds=[0, 1]).add(F).show()[[0.19151945 0.62210877 0.43772774 0.78535858 0.77997581 0.27259261]]

様々なカスタマイズが可能です。
plot = Petal(bounds=[0, 1],
cmap="tab20",
labels=["profit", "cost", "sustainability", "environment", "satisfaction", "time"],
title=("Solution A", {'pad': 20}))
plot.add(F)
plot.show()
ペタル図を並べて配置することで,解ごとのトレードオフを比較できます。
F = np.random.random((6, 6))
plot = Petal(bounds=[0, 1], title=["Solution %s" % t for t in ["A", "B", "C", "D", "E", "F"]])
plot.add(F[:3])
plot.add(F[3:])
plot.show()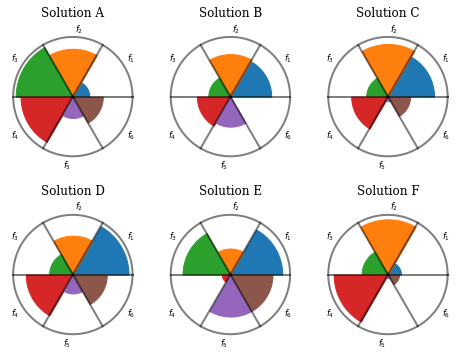
| 主な引数 | 説明 |
| bounds | 各軸の上下限値 (tuple) |
| axis_style | 軸スタイル(e.g. color, alpha…)(dict) |
| reverse | デフォルトはFalse, Trueだと面積が大きいほど値が小さくなる (bool) |
| figsize | 図のサイズ (tuple) |
| title | 図のタイトル (str or tuple) |
| legend | 凡例を表示するか (bool) |
| tight_layout | サブプロット間を調節するか (bool) |
| cmap | カラーマップ (colormap) |
5.1.5 Radar (レーダーチャート)
解ごとのトレードオフの比較には,レーダーチャートも使用可能です。
各項目の上下限値を設定します。正規化しない場合,内側の図形は下限値を示します。
import numpy as np
from pymoo.visualization.radar import Radar
np.random.seed(3)
ideal_point = np.array([0.15, 0.1, 0.2, 0.1, 0.1])
nadir_point = np.array([0.85, 0.9, 0.95, 0.9, 0.85])
F = np.random.random((1, 5)) * (nadir_point - ideal_point) + ideal_point
print(F)
plot = Radar(bounds=[ideal_point, nadir_point], normalize_each_objective=False)
plot.add(F)
plot.show()[[0.53555853 0.66651826 0.41817855 0.50866208 0.76971022]]

normalize_each_objective を True とすることで,正規化が可能です。(デフォルトはTrue)正規化すると,下限値が中心点となります。
plot = Radar(bounds=[ideal_point, nadir_point], normalize_each_objective=True)
plot.add(F)
plot.show()
ペタル図を並べて配置することで,解ごとのトレードオフを比較できます。
F = np.random.random((6, 5)) * (nadir_point - ideal_point) + ideal_point
plot = Radar(bounds=[ideal_point, nadir_point],
axis_style={"color": 'blue'},
point_style={"color": 'red', 's': 30})
plot.add(F[:3], color="red", alpha=0.8)
plot.add(F[3:], color="green", alpha=0.8)
plot.show()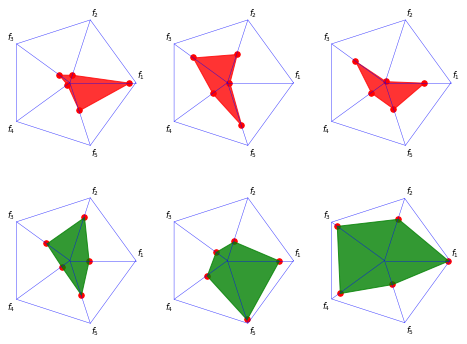
| 主な引数 | 説明 |
| bounds | 各軸の上下限値 (tuple/list/numpy.array) e.g. bounds=[[1,1,1,2,2,5],[32,32,32,32,32,32]] |
| normalize_each_objective | 各オブジェクトを正規化するかどうか (bool) |
| point_style | 点スタイル (dict) |
| n_partitions | レーダーに表示するパーティションの数 (int) |
| reverse | 正規化されている場合に使用可能 (bool) True の場合 1-input の値を出力 |
| axis_style | 軸スタイル (dict) |
| labels | 軸ラベル (str or list) |
| figsize | 図のサイズ (tuple) |
| title | 図のタイトル (str or tuple) |
| legend | 凡例を表示するか (bool) |
| tight_layout | サブプロット間を調節するか (bool) |
| cmap | カラーマップ (colormap) |
5.1.6 Radviz
Radviz は高次元データを2次元平面に写像して可視化します。参考
from pymoo.problems import get_problem
from pymoo.util.ref_dirs import get_reference_directions
from pymoo.visualization.radviz import Radviz
ref_dirs = get_reference_directions("uniform", 6, n_partitions=5)
F = get_problem("dtlz1").pareto_front(ref_dirs)
Radviz().add(F).show()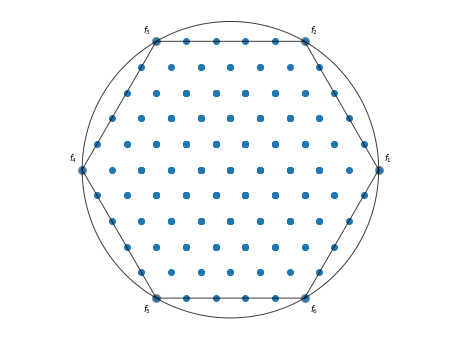
様々なカスタマイズが可能です。
plot = Radviz(title="Optimization",
legend=(True, {'loc': "upper left", 'bbox_to_anchor': (-0.1, 1.08, 0, 0)}),
labels=["profit", "cost", "sustainability", "environment", "satisfaction", "time"],
endpoint_style={"s": 70, "color": "green"})
plot.set_axis_style(color="black", alpha=1.0)
plot.add(F, color="grey", s=20)
plot.add(F[65], color="red", s=70, label="Solution A")
plot.add(F[72], color="blue", s=70, label="Solution B")
plot.show()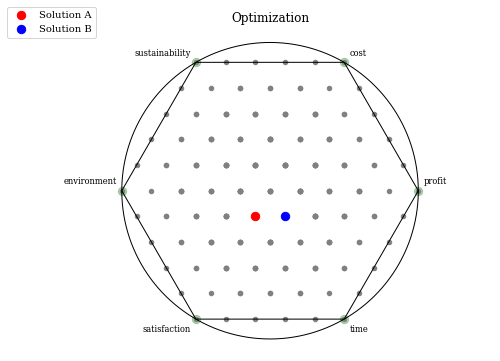
| 主な引数 | 説明 |
| axis_style | 軸スタイル(e.g. color, alpha…)(dict) |
| endpoint_style | endpointのスタイル (dict)* |
| labels | 軸ラベル (str or list) |
| figsize | 図のサイズ (tuple) |
| title | 図のタイトル (str or tuple) |
| legend | 凡例を表示するか (bool) |
| tight_layout | サブプロット間を調節するか (bool) |
| cmap | カラーマップ (colormap) |
5.1.7 Star Coordinates
Star Coordinates は高次元データを2次元平面に写像して可視化します。Radviz とは異なり,プロットが円の外側になることもあります。
from pymoo.problems import get_problem
from pymoo.util.ref_dirs import get_reference_directions
from pymoo.visualization.radviz import Radviz
ref_dirs = get_reference_directions("uniform", 6, n_partitions=5)
F = get_problem("dtlz1").pareto_front(ref_dirs)
Radviz().add(F).show()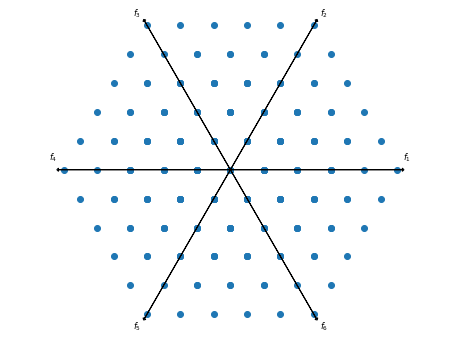
様々なカスタマイズが可能です。
plot = Radviz(title="Optimization",
legend=(True, {'loc': "upper left", 'bbox_to_anchor': (-0.1, 1.08, 0, 0)}),
labels=["profit", "cost", "sustainability", "environment", "satisfaction", "time"],
endpoint_style={"s": 70, "color": "green"})
plot.set_axis_style(color="black", alpha=1.0)
plot.add(F, color="grey", s=20)
plot.add(F[65], color="red", s=70, label="Solution A")
plot.add(F[72], color="blue", s=70, label="Solution B")
plot.show()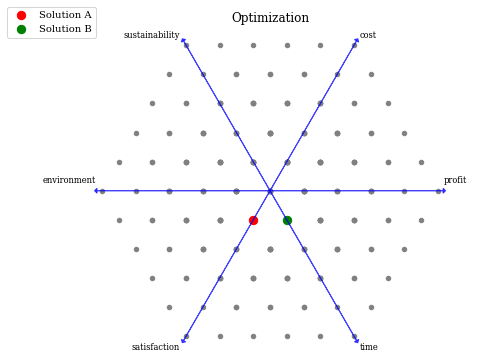
| 主な引数 | 説明 |
| axis_style | 軸スタイル(e.g. color, alpha…)(dict) |
| endpoint_style | endpointのスタイル (dict)* |
| labels | 軸ラベル (str or list) |
| figsize | 図のサイズ (tuple) |
| title | 図のタイトル (str or tuple) |
| legend | 凡例を表示するか (bool) |
| tight_layout | サブプロット間を調節するか (bool) |
| cmap | カラーマップ (colormap) |
5.2 収束性の検討
アルゴリズムの収束 (Convergence)について検討することで,様々な知見が得られます。
収束を確認するための方法として,pymooではアルゴリズム全体の履歴 (History)を保存する方法と,Callback オブジェクト(4.1.2項参照)を用いる方法の二つが存在します。
5.2.1 History
minimize 関数を呼び足す際に,save_history フラグを有効にすることで,アルゴリズムの履歴を保存することができます。
多くのメモリを消費するため,世代数が少なかったり,オブジェクトに大量のデータが含まれていないアルゴリズムでのみ使用可能です。
from pymoo.algorithms.soo.nonconvex.ga import GA
from pymoo.problems import get_problem
from pymoo.optimize import minimize
import numpy as np
import matplotlib.pyplot as plt
problem = get_problem("ackley")
algorithm = GA()
res = minimize(problem,
algorithm,
termination=('n_gen', 10),
seed=1,
save_history=True)
n_evals = np.array([e.evaluator.n_eval for e in res.history])
opt = np.array([e.opt[0].F for e in res.history])
plt.title("Convergence")
plt.plot(n_evals, opt, "--")
plt.xlabel("Number of evaluations")
plt.ylabel("Fitness")
plt.show()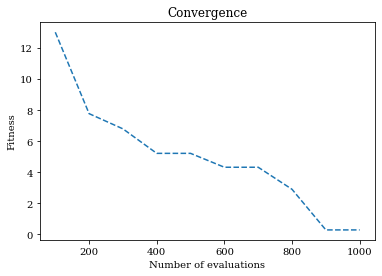
res.history には各世代の Algorithm オブジェクトが格納されます。
| 変数(nは任意の世代数) | 戻り値 |
| res.history[n].termination | Termination オブジェクト(3章) |
| res.history[n].display | Display オブジェクト(4.1.1項) |
| res.history[n].callback | Callback オブジェクト(4.1.2項) |
| res.history[n].problem | 問題の詳細情報 |
| res.history[n].return_least_infeasible | return_least_infeasible の設定 |
| res.history[n].save_history | save_history の設定 |
| res.history[n].verbose | verbose の設定 |
| res.history[n].seed | 乱数シードの設定 |
| res.history[n].default_ternination | デフォルトの終了条件 |
| res.history[n].has_terminated | アルゴリズムが終了したか否か |
| res.history[n].pf | パレートフロントが存在or超えたかどうか |
| res.history[n].evaluator.n_eval | 評価個体数 |
| res.history[n].n_gen | 世代数 |
| res.history[n].history | History オブジェクト |
| res.history[n].pop | 母集団全ての Individual オブジェクト |
| res.history[n].opt[0] | 最適解の Individual オブジェクト |
| res.history[n].data | サブモジュールの追加データ |
| res.history[n].is_initialized | 初期化メソッドの設定 |
| res.history[n].start_time | Algorithm オブジェクトが設定された時間 |
Individual オブジェクト
Individual オブジェクトには,各個体の属性が格納されています。
各属性の値は次のように呼び出せます。
res.history[5].opt[0].Xarray([-0.77879758, -1.04656146])
| 主な属性 | 戻り値 |
| X | 入力変数 |
| F | 目的変数 |
| CV | 制約違反量 |
| G | 制約条件 |
| feasible | 実行可能解かどうか |
| data | その他の情報 |
5.3 アルゴリズムの性能評価
トレードオフの関係にある複数の評価関数を最適化すると,最適解がパレート解として複数得られるため,大域的最適解までの距離を単純には定義できません。また,実際問題では大域的最適解が不明な場合もあり,アルゴリズムの性能評価方法を適切に選択する必要があります。
pymooでは様々なアルゴリズムの性能評価方法が実装されています。それぞれの原論文などはこちらを参照してください。
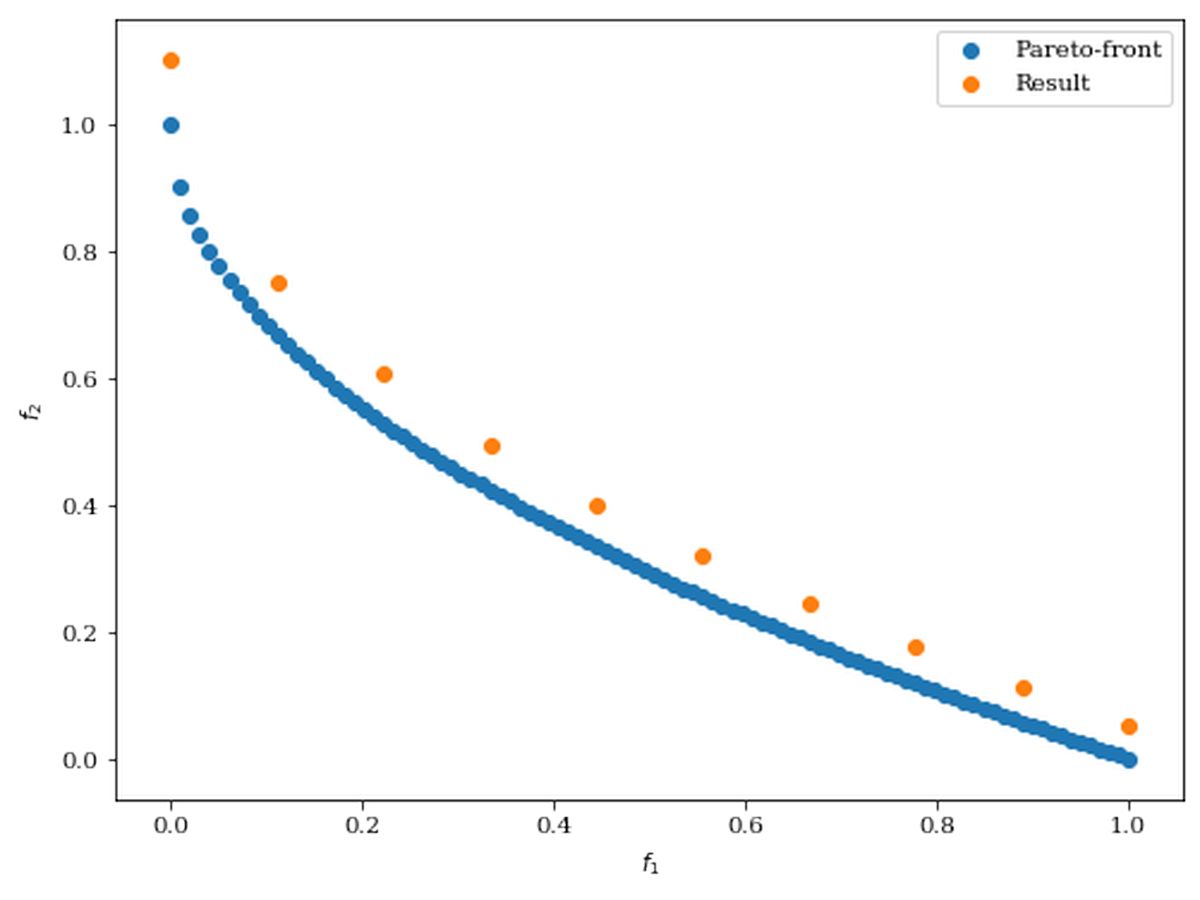
次のように最適化計算結果が与えられた場合を考えます。
import numpy as np
from pymoo.problems import get_problem
from pymoo.visualization.scatter import Scatter
# zdt1のパレートフロント
pf = get_problem("zdt1").pareto_front()
# アルゴリズムにより得られた結果
A = pf[::10] * 1.1
# 結果の描画
Scatter(legend=True).add(pf, label="Pareto-front").add(A, label="Result").show()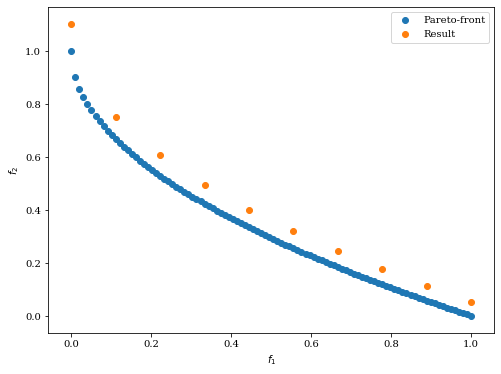
5.3.1 Generational Distance (GD)
GD は得られた解から参照点集合までの距離を測定します。アルゴリズムにより得られた解集合を $A=\{ a_{1},a_{2},…,a_{|A|}\}$ とし,参照点集合(明らかならばパレートフロント)を $Z=\{ z_{1},z_{2},…,z_{|Z|}\}$ とすると,GD は次式で計算できます。
$$GD\left(A\right)=\frac{1}{\left|A\right|}\left(\sum_{i=1}^{\left|A\right|} d^{p}_{i}\right)^{1/p}$$
ここで,$d_{i}$ は $a_{i}$ と $a_{i}$ から最も近い参照点 $z_{i}$ までのユークリッド距離(p=2)です。GD は解集合 $A$ から参照点集合 $Z$ 内の最近傍点までの平均距離を表します。
from pymoo.indicators.gd import GD
ind = GD(pf)
print("GD", ind(A))GD 0.05497689467314528
5.3.2 Generational Distance Plus (GD+)
GD+ は GD の距離計算を修正した評価指標です。得られた最適解が参照点集合(パレートフロントでない)を超える場合に距離を0とします。
$$GD^{+}\left(A\right)=\frac{1}{\left|A\right|}\left(\sum_{i=1}^{\left|A\right|} {d^{+}_{i}}^{2}\right)^{1/2}$$
ここで,$d^{+}_{i}=\max\left(a_{i}-z_{i},0\right)$ です。
from pymoo.indicators.gd_plus import GDPlus
ind = GDPlus(pf)
print("GD+", ind(A))GD+ 0.05497689467314528
5.3.3 Inverted Generational Distance (IGD)
IGD は GD とは逆に $Z$ の任意の点から $A$ 内の最近傍点までの距離を計算します。
$$IGD\left(A\right)=\frac{1}{\left|Z\right|}\left(\sum_{i=1}^{\left|Z\right|} {\hat{d_{i}}}^{p}\right)^{1/p}$$
ここで,$\hat{d_{i}}$ は $z_{i}$ と $z_{i}$ から最も近い参照点 $a_{i}$ までのユークリッド距離(p=2)です。IGD は参照点集合 $Z$ から解集合 $A$ 内の最近傍点までの平均距離を表す。
from pymoo.indicators.igd import IGD
ind = IGD(pf)
print("IGD", ind(A))IGD 0.06690908300327662
5.3.4 Inverted Generational Distance Plus (IGD+)
IGD+ は IGD の距離計算を GD+ と同様に修正した評価指標です。
$$IGD^{+}\left(A\right)=\frac{1}{\left|Z\right|}\left(\sum_{i=1}^{\left|Z\right|} {d^{+}_{i}}^{2}\right)^{1/2}$$
ここで,$d^{+}_{i}=\max\left(a_{i}-z_{i},0\right)$ です。
from pymoo.indicators.igd_plus import IGDPlus
ind = IGDPlus(pf)
print("IGD+", ind(A))IGD+ 0.06466828842775944
5.3.5 Hypervolume (HV)
5.3.4項までの指標は全て参照点集合(パレートフロントなど)が必要でした。Hypervolume は参照点集合が未知の場合に使用できる評価指標です。
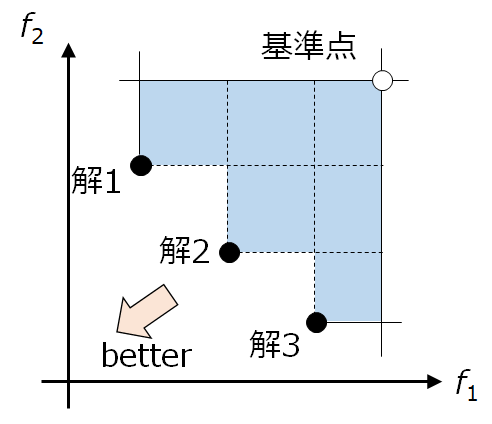
Hypervolume では,まず基準点を設定します。そして,基準点を基準に,アルゴリズムにより得られた解によってパレート支配される領域(2次元なら矩形領域,3次元なら直方体)の総計を計算します。
from pymoo.indicators.hv import HV
ref_point = np.array([1.2, 1.2])
ind = HV(ref_point=ref_point)
print("HV", ind(A))HV 0.9631646448182305
5.3.6 Running Metric
Running Metric (論文) もパレートフロントが不明な場合の分析方法です。ある特定の世代の集団を参照点集合として各世代の IGD を計算,アルゴリズムの生存率を使って改善度合いを可視化します。
import numpy as np
from pymoo.problems import get_problem
from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.optimize import minimize
from pymoo.util.running_metric import RunningMetricAnimation
problem = get_problem("zdt1")
algorithm = NSGA2(pop_size=50)
res = minimize(problem,
algorithm,
('n_gen', 40),
seed=1,
verbose=False,
save_history=True)
running = RunningMetricAnimation(delta_gen=10,
n_plots=4,
key_press=False,
do_show=True)
for algorithm in res.history:
running.update(algorithm)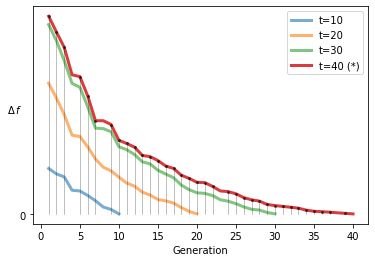
以上です。
修正点等ございましたら,コメント欄,メールやTwitterよりお知らせください。