なぜ2極3スロット/4極3スロットのPMSMではロータの回転方向が逆になるのか？

一年以上前にこんなアンケートをとった。

@モータに関わる技術者各位

一般の技術理解水準が知りたく、アンケートにご協力お願いします。

磁石同期モータで、2極3スロットと4極3スロットでは、ステータ回転磁界とロータ回転方向が逆転する、ということを

— 清水 悠生/Yuki Shimizu (@YuYuMoYuYu) April 21, 2024

極スロコンビネーションに対する同期モータの回転原理を、モータに関わる技術者はほとんど知らないらしい。
かく言う私も、ドクターの学生のころ(?)に赤津先生に飲みの場で「3スロモータで2極と4極とでは回転方向が異なるんだよ。なんでか分かるか？」と言われて即答できなかった。当時は自動車用の8極48スロットという素直なモータばかりやっていたせいもある。

コロナが明けていろんな企業技術者、大学研究者に聞いて回ってみたが、モータの設計開発で集中巻の分数スロットモータを扱っている人でも、結構この質問に答えられない人が多かった。このあたりの理論が、物理的直観的な解釈が難しいからかもしれない。

最近も極スロコンビネーションについて考える機会があったので、思考を整理する。

理論

前提は、3スロット、3相平衡・時間高調波なしのモータ。起磁力はステップ上に分布すると仮定。

• 機械角：$\theta\in[0,2\pi)$
• 各相コイルの配置（中心位置）：$\theta_u=0,\ \theta_v=\tfrac{2\pi}{3},\ \theta_w=\tfrac{4\pi}{3}$
• 各相巻線の空間分布（簡易ver）：

$$g(\theta)= \begin{cases} 1,& |\theta|<\pi/3,\\ 0,& \text{それ以外}. \end{cases} \qquad g_u(\theta)=g(\theta-\theta_u),\ g_v(\theta)=g(\theta-\theta_v),\ g_w(\theta)=g(\theta-\theta_w),$$

• 三相平衡電流（時間高調波なし）：

$$i_u=\cos \omega t,i_v=\cos \text{\hspace{0.17em}⁣}(\omega t-\frac{2\pi }{3}),i_w=\cos \text{\hspace{0.17em}⁣}(\omega t-\frac{4\pi }{3})\mathrm{.}$$

この前提の場合、ステータの起磁力（MMF）はこうなる。

$$\boxed{{\displaystyle F(\theta ,t)=i_u(t)g_u(\theta )+i_v(t)g_v(\theta )+i_w(t)g_w(\theta )}}$$

注意されたいのが、時間高調波はないが空間高調波はある、という点。巻線関数が正弦波ではないので。これを可視化したのが以下。空間FFTの1~3次の結果ものせている。

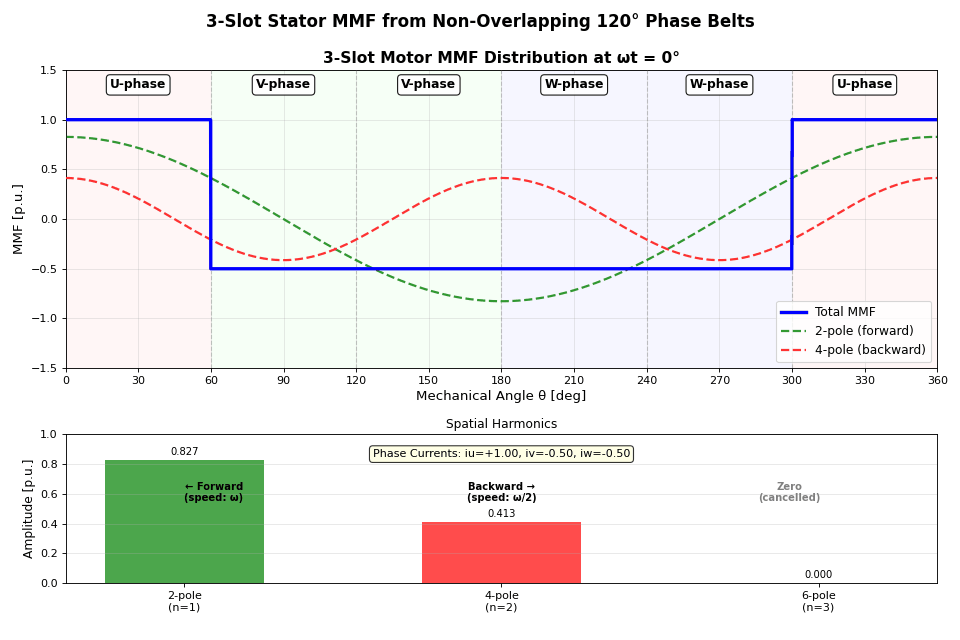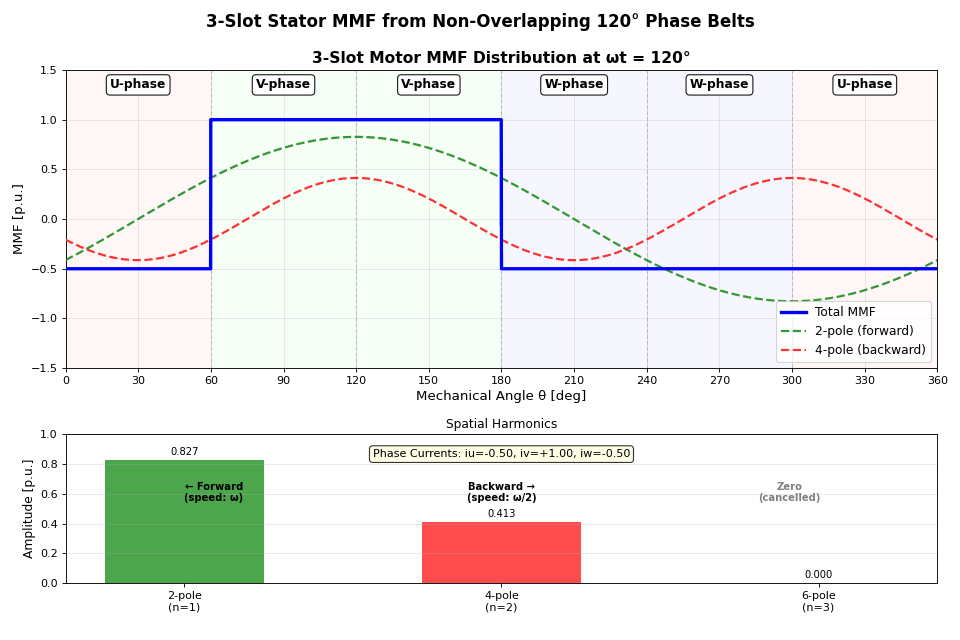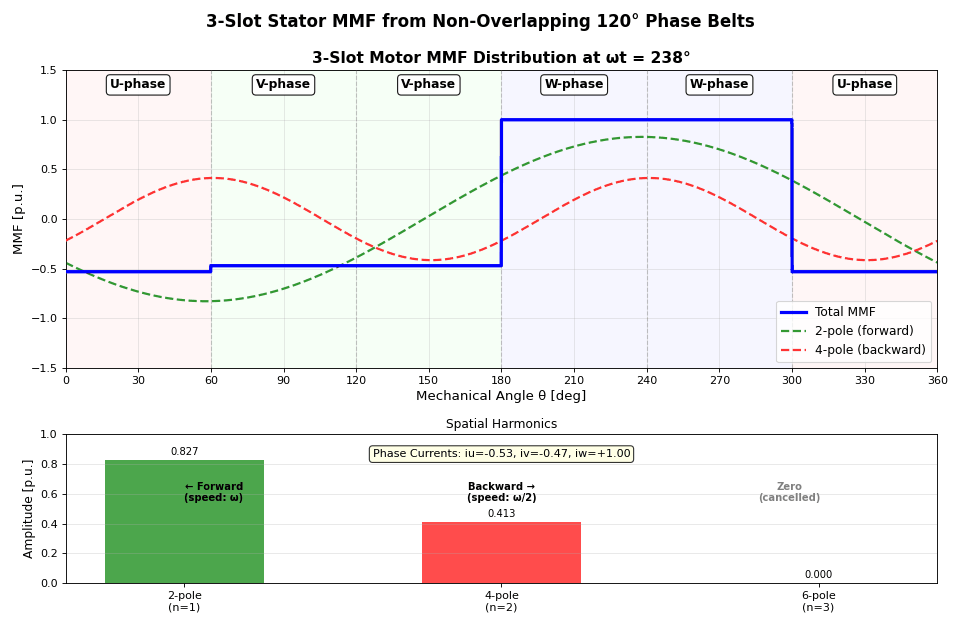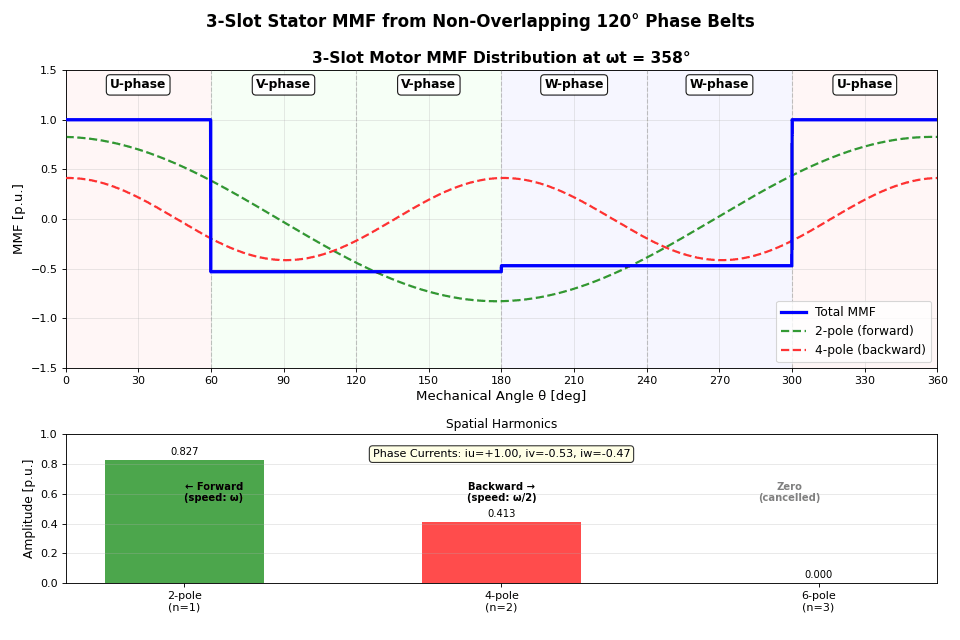
コードはこちらに。

GitHub - yshimizu12/mmf_visualization: mmf_visualization

mmf_visualization. Contribute to yshimizu12/mmf_visualization development by creating an account on GitHub.

github.com

なぜ2極/4極で逆回転するか？

そもそも同期モータは、ステータ回転磁界とロータが同期して回転する。その同期対象は、ロータの極数が2（N,S）ならステータ起磁力の基本波（動画の緑破線）、極数が4（N,S,N,S）ならステータ起磁力の2次高調波（動画の赤破線）である。これは、同じ周波数成分でなければ、トルクの1周分の平均が0になるからである。

動画を見ると、ステータ起磁力の2次高調波は基本波に対して逆方向、かつ、半分のスピードで回転する。これが、2極/4極のロータが逆回転する理由である。同期対象がそうなっているから、ということだ。

ちなみにステータ起磁力の3次高調波は存在しない。そのため、6極のロータはそもそも回転しない。直感的には、例えば60-180°区間など、空間3次に相当する一周区間でMMFは一定値を取り、そもそも3次高調波として現れる成分が存在しない（3次高調波成分に直交する）。これは3n次高調波にも言えることなので、6n極のロータではトルクが発生しない。

なぜステータ起磁力の1,2次成分は逆方向に進むのか？

これを理解するのがなかなか難しい。FFTしたらそうなったから、と言ってしまえばそれで終わり。

一応私はωのワルツ的に理解している。

数学ガール

結城浩『数学ガール』（数学ガールシリーズ1）

www.hyuki.com

まず、ステータの巻線分布を複素数平面で捉える。3スロの相中心は機械角で $0^\circ,120^\circ,240^\circ$。
ここで、1の3乗根 $\displaystyle \omega=e^{j\frac{2\pi}{3}}$ を使うと、空間内のuvw相巻線は以下のベクトルと等価。

$$\boxed{{\displaystyle [1,\omega ,{\omega }^2]}}$$

この場合の起磁力は、以下に比例する。（このベクトルは、各相巻線の空間分布全体ではない）

そして、巻線ベクトルを、電気角（ロータ側からの視点）で捉える。ロータの極対数を $p$ とすると、機械角を電気角に変換することは、各相の位相を $p$ 倍するのと等価なので、空間内のuvw相巻線は

$$\boxed{\;[\,1,\ \omega^p,\ \omega^{2p}\,]\;}$$

のように捉えられる。（$\displaystyle \omega=e^{j\frac{2\pi}{3}}$となっただけ。）

極数を変えていくと、このベクトルは以下のふるまいをする。

$$[\,1,\ \omega^p,\ \omega^{2p}\,]\ = \begin{cases} [\,1,\ \omega,\ \omega^2\,], & p\equiv 1\pmod{3}\ \ \ (\textbf{正相＝順方向}),\\[4pt] [\,1,\ \omega^2,\ \omega\,], & p\equiv 2\pmod{3}\ \ \ (\textbf{逆相＝逆方向}),\\[4pt] [\,1,\ 1,\ 1\,], & p\equiv 0\pmod{3}\ \ \ \ \ \ \ \ \ \ (\textbf{ゼロ＝回らない}). \end{cases}$$

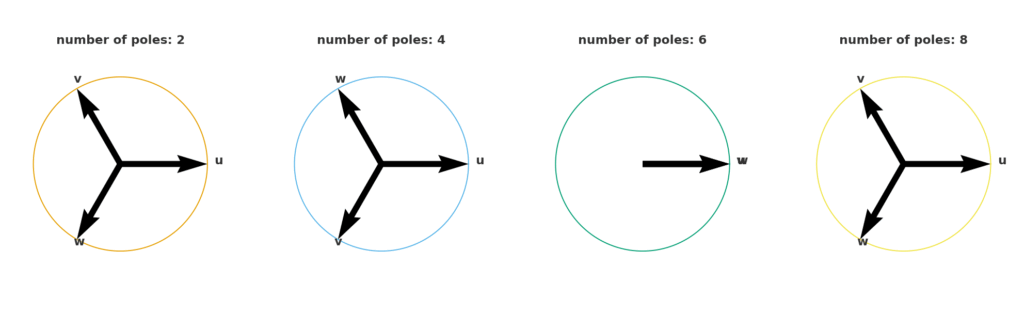
2極ならu→v→w、4極ならu→w→vの順番なので、逆回転。6極の[1,1,1]は零相を意味し、三相平衡では、以下のように同期成分が打ち消される。$$i_u+i_v+i_w=0 \quad\Rightarrow\quad i_u\cdot1+i_v\cdot1+i_w\cdot1=0$$

このアイデアのよいところは、多相多極多スロにも拡張性がある点。多相はそのままベクトルの数を増やせばよい。多スロは分数スロットのときが少しややこしいが、電気角1周期あたりのスロット数Lを考えると、Lが3の倍数なら回るし、そうでないなら回らない。回転方向は多スロでも（時間高調波を無視した場合） $p$ のmod 3で求まる。Lの具体的な定義は以下の通り。

$$\boxed{\,L=\frac{S}{\gcd(S,\;p)}\,}$$

ここで、S：スロット数、$p$：極対数、$\gcd$：最大公約数。最大公約数を使う理由について補足すると、まず1スロットあたりの電気角は以下の通り。

$$\mathrm{\Delta }{\theta }_e=\frac{2\pi }{S}\times p$$

今求めたいのは、電気角でちょうど1周期（$2\pi$）に一致するようなスロット数 $n$なので、

$$n\,\Delta\theta_e=2\pi\ell\quad\Longleftrightarrow\quad n\,p=\ell\,S.$$このとき、最小の正の整数 $n$ を求めると、

$$\boxed{{\displaystyle n=\frac{S}{\gcd (S,p)}}}$$

となり、これがそのまま電気角1周期あたりのスロット数 $L$$である$。

数学的には理解できるが、物理現象からはかけ離れてしまうのが難点。もっといい捉え方があったら教えてほしい。