ガウス過程回帰 (Gaussian Process Regression)は,予測が確率分布(ガウス分布)で与えられ,分散の値から予測のばらつき具合も評価することができます。背景にあるガウス過程は様々な分野で研究されており,クリギングやカルマンフィルタ,ニューラルネットワークなど多くの手法に関連するモデルです。本記事では,ガウス過程回帰の定義と解釈について解説します。
pythonによるサンプルプログラムはこちらからどうぞ。
大きい画面で表示したい方はこちらからご覧ください。
スライドの目次
- 本記事の内容と対象
- ①ガウス分布とは
- ガウス分布(正規分布)とは
- 標準偏差と確率
- 分散のイメージ
- 2次元のガウス分布
- 共分散のイメージ
- N次元のガウス分布(多変量正規分布)
- ②ガウス過程回帰をざっくり理解する
- 回帰分析の前提
- 最小二乗法の場合
- ガウス過程回帰の場合
- ガウス過程回帰の特徴
- ガウス過程回帰のざっくりまとめ
- ③ガウス過程とは
- ガウス過程の定義
- 線形回帰モデルの引用
- 非線形写像
- 重みをガウス分布に従って生成
- 出力ベクトルの平均と共分散行列
- まとめると…
- 出力データの平均は0でよいのか?
- ガウス過程の共分散行列の解釈
- カーネル関数の導入
- ④ガウス過程を用いた回帰分析
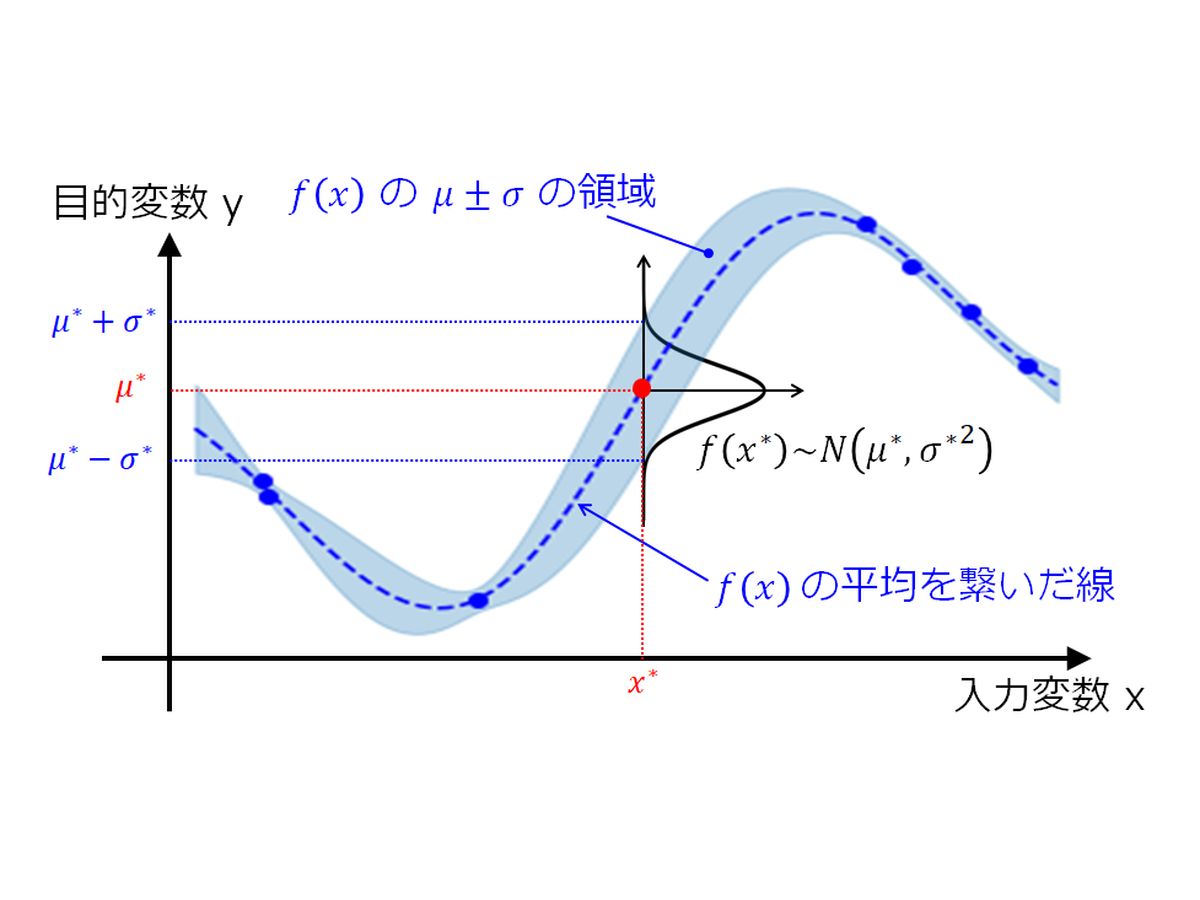
- 未知のデータをどう予測するか?
- 最小二乗法なら簡単
- ガウス過程では一筋縄ではいかない
- 未知の入力データを含んだ分布を考える
- 予測分布の期待値と分散の解釈
参考文献
- C.M. ビショップ,パターン認識と機械学習 上, 丸善出版 (2012)
- C.M. ビショップ,パターン認識と機械学習 下, 丸善出版 (2012)
- 持橋大地・大羽成征,ガウス過程と機械学習,講談社 (2019)
質問、コメント等ございましたら、下部のコメント欄,もしくはメールやTwitterよりご連絡ください。