最小二乗法を用いた回帰分析ー②重回帰分析と非線形回帰分析ー【Pythonプログラム付】

統計や機械学習において最も基本的な回帰分析手法は（通常）最小二乗法（OLS：Ordinary Least Squares）です。その中でも説明変数(x)が一つしかない回帰分析を単回帰分析といいます。

統計や機械学習において最も基本的な回帰分析手法は（通常）最小二乗法（OLS：Ordinary Least Squares）です。その中でも説明変数(x)が一つしかない単回帰分析は，Microsoft Excelの「近似曲線」機能etcで使用...

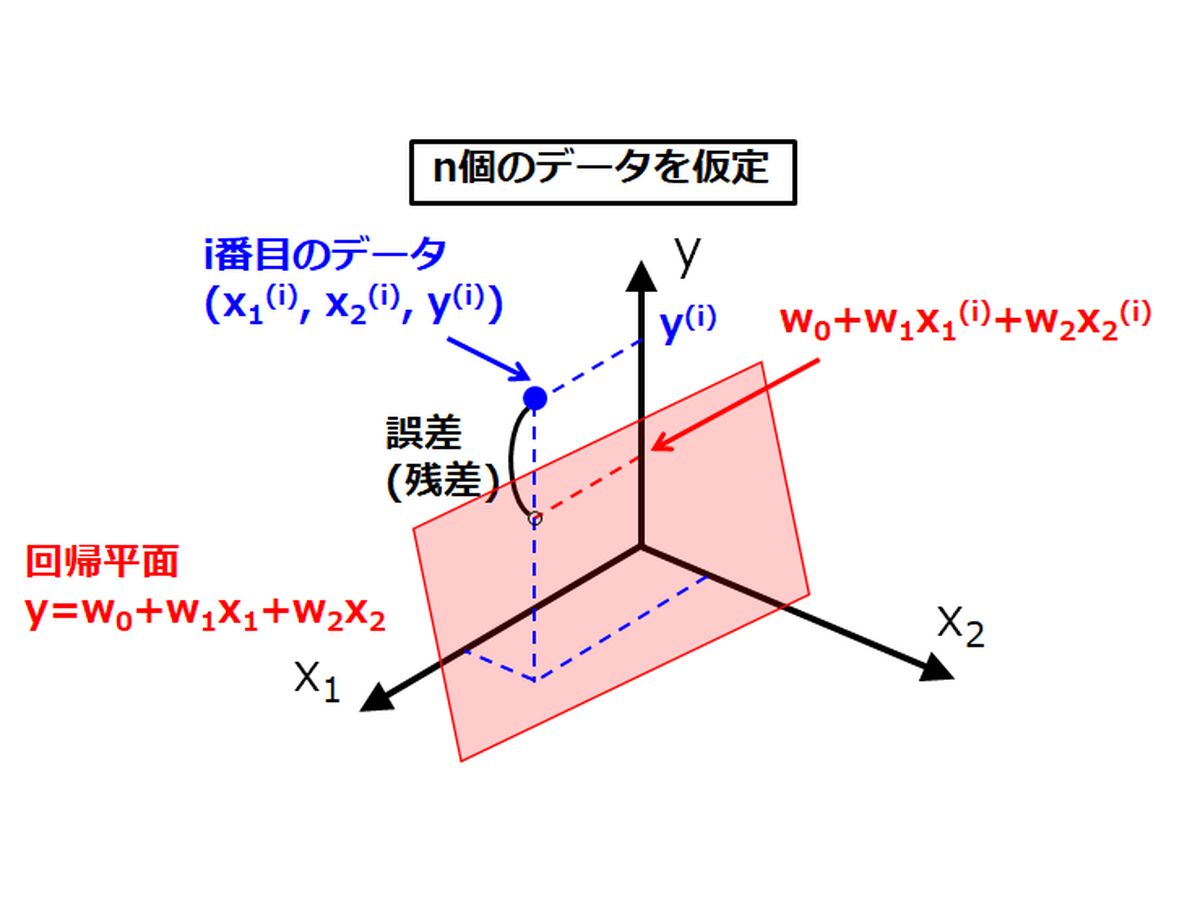
しかし，現実にある様々な事象は複数の因子によって記述されることがほとんどであり，説明変数が複数である重回帰分析が必要となります。本記事では，最小二乗法を用いた単回帰分析から重回帰分析への拡張や重回帰分析を使用することができない多重共線性（マルチコ，Multicollinearity），線形回帰分析から非線形回帰分析への拡張について説明します。

pythonによるサンプルプログラムはこちらからどうぞ。

大きい画面で表示したい方はこちらからご覧ください。