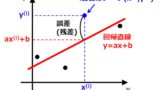
統計や機械学習において最も基本的な回帰分析手法は（通常）最小二乗法（OLS：Ordinary Least Squares）です。
最小二乗法を用いた回帰分析ー①線形単回帰分析ー【Pythonプログラム付】
統計や機械学習において最も基本的な回帰分析手法は（通常）最小二乗法（OLS：Ordinary Least Squares）です。その中でも説明変数(x)が一つしかない単回帰分析は，Microsoft Excelの「近似曲線」機能etcで使用...
yuyumoyuyu.com
2020.12.13
しかし，データの量や性質によっては回帰係数がデータに過度に適合する過学習が生じる可能性があり，回帰曲線の汎化性能が著しく低下する場合があります。そこで登場するのが，正則化項を導入した正則化最小二乗法（Regularized Least Squares）です。本記事では，過学習のイメージから正則化項の導入，最も有名なリッジ回帰やlassoについて解説します。
大きい画面で表示したい方はこちらからご覧ください。
pythonによるサンプルプログラムはGitHubで公開しています。
スライドの目次
- はじめに
- (復習)最小二乗法で扱う誤差関数
- 多項式回帰の例
- 過学習とは
- 過学習の際の係数の値
- 正則化項の導入
- 正則化項を導入した際の回帰曲線
- 正則化項を導入した際の回帰係数
- 誤差関数の幾何学的解釈
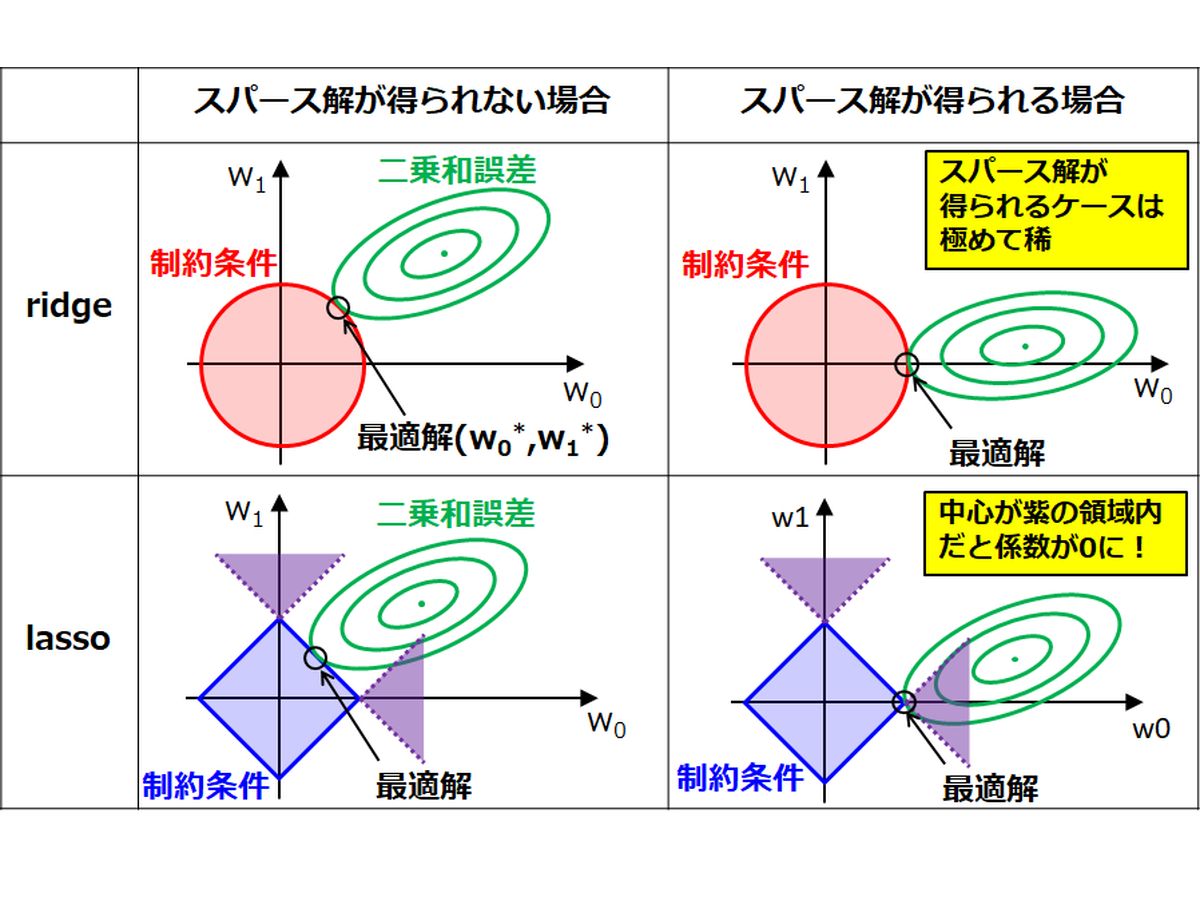
- なぜlassoはスパース解が得られやすいのか
参考文献
- C.M. ビショップ，パターン認識と機械学習 上, 丸善出版 (2012)
質問、コメント等ございましたら、下部のコメント欄，もしくはメールやTwitterよりご連絡ください。
