逐次最小二乗法（RLS: Recursive Least Squares）ーパラメータ同定に用いられる時系列データの回帰手法！ー

制御関連の業務では時系列のデータを主に扱い，時系列データから各種パラメータを同定したい場面は数多く存在します。パラメータ同定のための最も簡単な手法は，通常最小二乗法（OLS：Ordinary Least Squares）です。

統計や機械学習において最も基本的な回帰分析手法は（通常）最小二乗法（OLS：Ordinary Least Squares）です。その中でも説明変数(x)が一つしかない単回帰分析は，Microsoft Excelの「近似曲線」機能etcで使用...

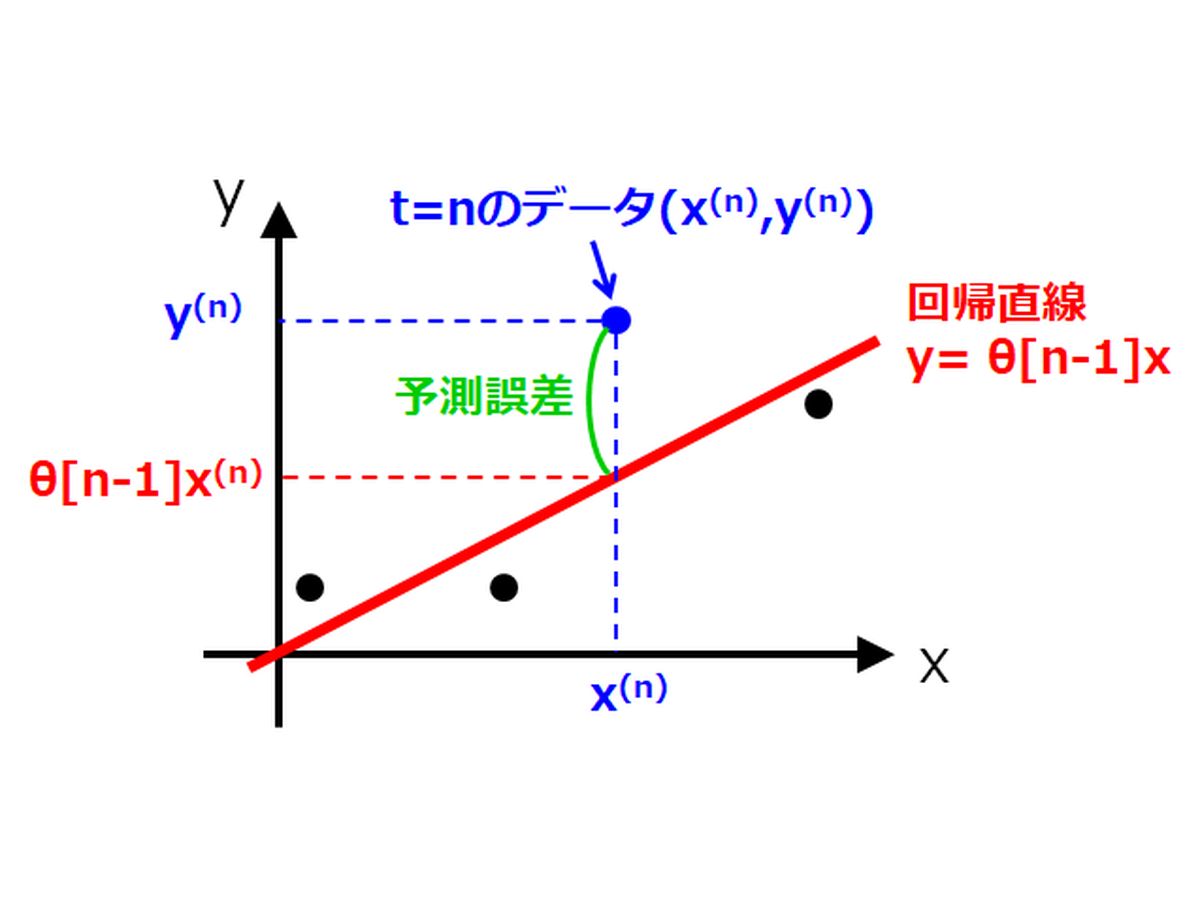
しかし，対象とするパラメータが時間により変動する場合には，通常最小二乗法では予測誤差が大きくなる場合があります。そこで登場するのが，忘却係数を導入した逐次最小二乗法（RLS: Recursive Least Squares）です。本記事では，逐次最小二乗法の誤差関数の定義から漸化式の導出まで解説します。

大きい画面で表示したい方はこちらからご覧ください。